
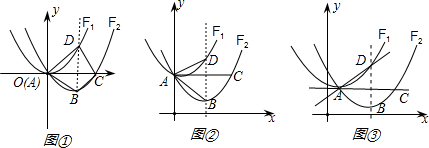
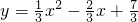 经过变换满足AC=2
经过变换满足AC=2 ,点P是直线AC上的动点,求点P到点D的距离与到直线AD的距离之和的最小值.
,点P是直线AC上的动点,求点P到点D的距离与到直线AD的距离之和的最小值. 解:(Ⅰ)将点C(2,0)的坐标代入抛物线F2的解析式,
解:(Ⅰ)将点C(2,0)的坐标代入抛物线F2的解析式, ,
,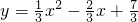 ,配方得
,配方得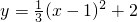 ,
, ,
, .
.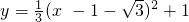 ,
, ,
,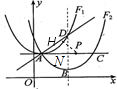
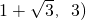 ,
, ,DB⊥AC,
,DB⊥AC,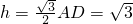 .
. .
. ,即可表示出△ABD的面积;
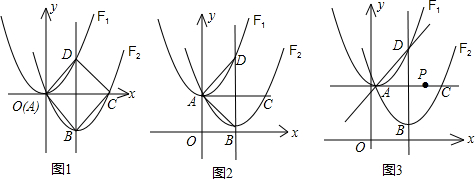
,即可表示出△ABD的面积; 的顶点坐标与对称轴,从而表示出F2的解析式,判断出四边形ABCD是菱形,要使PD+PH最小,即要使PB+PH最小,进而求出.
的顶点坐标与对称轴,从而表示出F2的解析式,判断出四边形ABCD是菱形,要使PD+PH最小,即要使PB+PH最小,进而求出.

科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| 1 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(33):2.3 二次函数的应用(解析版) 题型:解答题
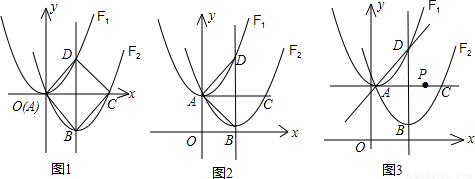
 x2-
x2- x+
x+ ,经过变换后,AC=2
,经过变换后,AC=2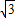 ,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.
,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷22(靖江初中 曹益军)(解析版) 题型:解答题
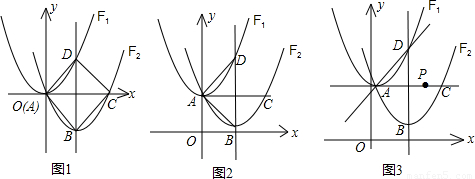
 x2-
x2- x+
x+ ,经过变换后,AC=2
,经过变换后,AC=2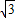 ,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.
,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com