
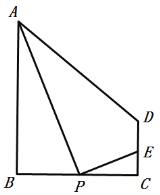
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .P为线段
.P为线段![]() 上的一动点,且和B、C不重合,连接
上的一动点,且和B、C不重合,连接![]() ,过点P作
,过点P作![]() 交射线
交射线![]() 于点E.
于点E.
聪聪根据学习函数的经验,对这个问题进行了研究:
(1)通过推理,他发现![]() ,请你帮他完成证明.
,请你帮他完成证明.
(2)利用几何画板,他改变![]() 的长度,运动点P,得到不同位置时,
的长度,运动点P,得到不同位置时,![]() 、
、![]() 的长度的对应值:
的长度的对应值:
当![]() 时,得表1:
时,得表1:
| … | 1 | 2 | 3 | 4 | 5 | … |
| … | 0.83 | 1.33 | 1.50 | 1.33 | 0.83 | … |
当![]() 时,得表2:
时,得表2:
| … | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| … | 1.17 | 2.00 | 2.50 | 2.67 | 2.50 | 2.00 | 1.17 | … |
这说明,点P在线段![]() 上运动时,要保证点E总在线段
上运动时,要保证点E总在线段![]() 上,
上,![]() 的长度应有一定的限制.
的长度应有一定的限制.
①填空:根据函数的定义,我们可以确定,在![]() 和
和![]() 的长度这两个变量中,_____的长度为自变量,_____的长度为因变量;
的长度这两个变量中,_____的长度为自变量,_____的长度为因变量;
②设![]() ,当点P在线段
,当点P在线段![]() 上运动时,点E总在线段
上运动时,点E总在线段![]() 上,求m的取值范围.
上,求m的取值范围.
【答案】(1)证明见解析;(2)①BP,CE;②0<m≤![]()
【解析】
(1)由同角的余角相等可得∠APB=∠CEP,又因为∠B=∠C=90°,即可证得相似;
(2)①由题意可得随着P点的变化,CE的长度在变化,即可判断自变量和因变量;
②设BP的长度为xcm,CE的长度为ycm,由△ABP∽△PCE,利用对应边成比例求出y与x的函数关系式,利用二次函数性质,求出其最大值,列不等式确定m的取值范围;
解:(1)证明:∵![]() ,
,
∴∠APE=90°,
∵∠APB+∠CPE=90°,∠CEP+∠CPE=90°,
∴∠APB=∠CEP,
又∵∠B=∠C=90°,
∴△ABP∽△PCE;
(2)①由题意可得随着P点的变化,CE的长度在变化,所以BP的长度为自变量,CE的长度为因变量;
故答案为:BP,CE;
②设BP的长度为xcm,CE的长度为ycm,
∵△ABP∽△PCE,
∴![]() ,即
,即![]() ,
,
∴y=![]()
=![]() ,
,
∴当x=![]() 时,y取得最大值,最大值为
时,y取得最大值,最大值为![]() ,
,
∵点P在线段BC上运动时,点E总在线段CD上,
∴![]() ≤2,
≤2,
解得m≤![]() ,
,
∴m的取值范围为:0<m≤![]() .
.


科目:初中数学 来源: 题型:
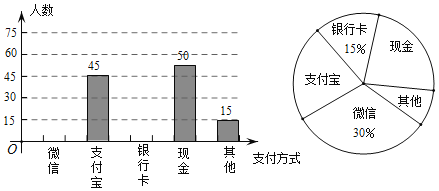
【题目】随着科技的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份“你最喜欢的支付方式”调查问卷(每人必选且只选一种),在某商场随机调查了部分顾客,并将统计结果绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人,在扇形统计图中,表示“现金”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是 ;
(3)运用这次的调查结果估计1000名顾客中用“支付宝”支付的有多少人?
(4)在一次购物中,嘉嘉和琪琪都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余活动情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方式收集数据(参与问卷调查的每名学生只能选择其中--项),并据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方式收集数据(参与问卷调查的每名学生只能选择其中--项),并据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
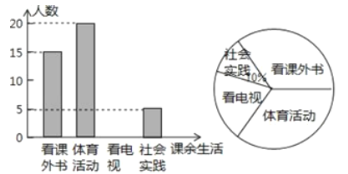
(1)![]() ,直接补全条形统计图;
,直接补全条形统计图;
(2)若该校共有学生![]() 名,试估计该校喜爱看课外书的学生人数;
名,试估计该校喜爱看课外书的学生人数;
(3)若被调查喜爱体育活动的![]() 名学生中有
名学生中有![]() 名男生和
名男生和![]() 名女生,现从这
名女生,现从这![]() 名学生中任意抽取
名学生中任意抽取![]() 名,请用列表或画树状图的方法求恰好抽到
名,请用列表或画树状图的方法求恰好抽到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火锅是重庆的一张名片,深受广大市民的喜爱.重庆某火锅店采取堂食、外卖、店外摆摊(简称摆摊)三种方式经营,6月份该火锅店堂食、外卖、摆摊三种方式的营业额之比为3:5:2.随着促进消费政策的出台,该火锅店老板预计7月份总营业额会增加,其中摆摊增加的营业额占总增加的营业额的![]() ,则摆摊的营业额将达到7月份总营业额的
,则摆摊的营业额将达到7月份总营业额的![]() ,为使堂食、外卖7月份的营业额之比为8:5,则7月份外卖还需增加的营业额与7月份总营业额之比是__________.
,为使堂食、外卖7月份的营业额之比为8:5,则7月份外卖还需增加的营业额与7月份总营业额之比是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点A在
,点A在![]() 上,四边形
上,四边形![]() 是矩形,连接
是矩形,连接![]() 、
、![]() 交于点E,连接
交于点E,连接![]() 交
交![]() 于点F.下列4个判断:①
于点F.下列4个判断:①![]() 平分
平分![]() ;②
;②![]() ;③
;③![]() ;④若点G是线段
;④若点G是线段![]() 的中点,则
的中点,则![]() 为等腰直角三角形.正确判断的个数是( )
为等腰直角三角形.正确判断的个数是( )

A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
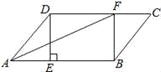
【题目】如图,在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=3,求DC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
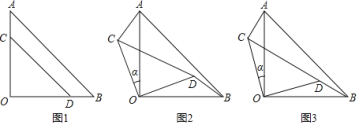
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=13,CD=7.保持纸片AOB不动,将纸片COD绕点O逆时针旋转a(0![]() α
α![]() 90°),如图2所示.当BD与CD在同一直线上(如图3)时,则△ABC的面积为____.
90°),如图2所示.当BD与CD在同一直线上(如图3)时,则△ABC的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
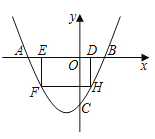
【题目】如图,抛物线y=ax2+(4a﹣1)x﹣4与x轴交于点A、B,与y轴交于点C,且OC=2OB,点D为线段OB上一动点(不与点B重合),过点D作矩形DEFH,点H、F在抛物线上,点E在x轴上.
(1)求抛物线的解析式;
(2)当矩形DEFH的周长最大时,求矩形DEFH的面积;
(3)在(2)的条件下,矩形DEFH不动,将抛物线沿着x轴向左平移m个单位,抛物线与矩形DEFH的边交于点M、N,连接M、N.若MN恰好平分矩形DEFH的面积,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2x+c与x轴交于点A(1,0),点B(﹣3,0),与y轴交于点C,连接BC,点P在第二象限的抛物线上,连接PC、PO,线段PO交线段BC于点 E.
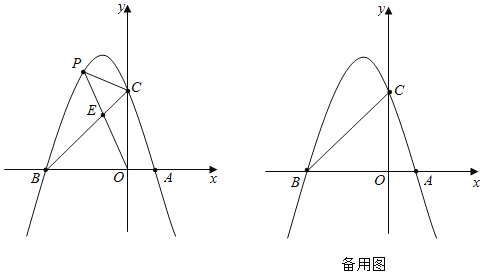
(1)求抛物线的表达式;
(2)若△PCE的面积为S1,△OCE的面积为S2,当![]() =
=![]() 时,求点P的坐标;
时,求点P的坐标;
(3)已知点C关于抛物线对称轴的对称点为点N,连接BN,点H在x轴上,当∠HCB=∠NBC时,
①求满足条件的所有点H的坐标;
②当点H在线段AB上时,点Q是线段BH外一点,QH=1,连接BQ,将线段BQ绕着点Q顺时针旋转90°,得到线段QM,连接MH,直接写出线段MH的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com