
【题目】如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( ).
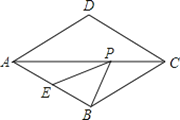
A. 1 B. 2 C. ![]() D.
D. ![]()
【答案】D
【解析】根据轴对称最短问题作法首先求出P点的位置,再结合菱形的性质得出△AEE′为等边三角形,进而求出PE+PB的最小值.
解:如图所示,
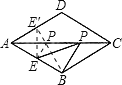
作E点关于AC对称点E′点,连接E′B,E′B与AC的交点即是P点,
∵菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,
∴AE′=AE=BE=1,∴△AEE′为等边三角形,∴∠AEE′=60°,
∴∠E′EB=120°,
∵BE=EE′,∴∠EE′B=30°,∴∠AE′B=90°,
BE′=![]() ,∵PE+PB=BE′,
,∵PE+PB=BE′,
∴PE+PB的最小值是: ![]() .
.
故答案为: ![]() .
.
“点睛”此题主要考查了菱形的性质以及轴对称中最短路径求法,正确地作出P点从而利用菱形性质得出是解决问题的关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形![]() ,求出阴影部分的面积及其边长.
,求出阴影部分的面积及其边长.
(3)把正方形![]() 放到数轴上,如图
放到数轴上,如图![]() ,使得
,使得![]() 与
与![]() 重合,点
重合,点![]() 与
与![]() 重合,点
重合,点![]() 与点
与点![]() 关于
关于![]() 点对称,那么
点对称,那么![]() 在数轴上表示的数为__________;点
在数轴上表示的数为__________;点![]() 在数轴上表示的数为__________.
在数轴上表示的数为__________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若直线y=2x+k﹣1经过第一、二、三象限,则k的取值范围是( )
A. k>1 B. k>2 C. k<1 D. k<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.腰对应相等的两个等腰三角形全等;B.等腰三角形角平分线与中线重合;
C.底边和顶角分别对应相等的两个等腰三角形全等;D.形状相同的两个三角形全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①“随意翻到一本书的某页,这页的页码一定是奇数”;②“明天太阳从东方升起”( )
A.只有①正确B.只有②正确C.①②都正确D.①②都错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )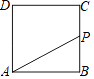
A.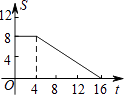
B.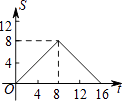
C.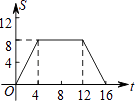
D.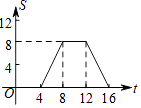
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com