
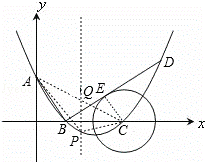
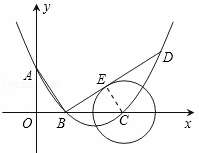
ͼ����ƽ��ֱ������ϵ�У�����Ϊ��4����1���������߽�y����A�㣬��x����B��C���㣨��B�ڵ�C����ࣩ����֪A������Ϊ��0��3����
��1����������ߵĽ���ʽ
��2������B���߶�AB�Ĵ��߽��������ڵ�D������Ե�CΪԲ�ĵ�Բ��ֱ��BD���У����ж������ߵĶԳ���l���C��������λ�ù�ϵ��������֤����
��3����֪��P���������ϵ�һ�����㣬��λ��A��C����֮�䣬�ʣ�����P�˶���ʲôλ��ʱ����PAC�������������ʱP�������͡�PAC����������



�⣺��1����������Ϊy=a��x��4��2��1��
�������߾�����A��0��3����
��3=a��0��4��2��1��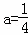 ��
��
��������Ϊ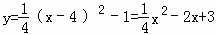 ����3�֣�
����3�֣�
��2���ཻ��
֤��������CE����CE��BD��
��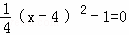 ʱ��x1=2��x2=6��
ʱ��x1=2��x2=6��
A��0��3����B��2��0����C��6��0����
�Գ���x=4��
��OB=2��AB=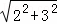 =
=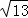 ��BC=4��
��BC=4��
��AB��BD��
���OAB+��OBA=90�㣬��OBA+��EBC=90�㣬
���AOB�ס�BEC��
��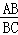 =
=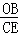 ����
����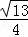 =
= �����CE=
�����CE=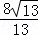 ��
��
��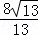 ��2��
��2��
�������ߵĶԳ���l���C�ཻ����7�֣�
��3����ͼ������P��ƽ����y���ֱ�߽�AC�ڵ�Q��
�����AC�Ľ���ʽΪ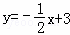 ����8�֣�
����8�֣�
��P���������m��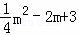 ����
����
��Q���������m��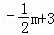 ����
����
��PQ=��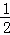 m+3����
m+3����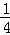 m2��2m+3��=��
m2��2m+3��=��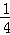 m2+
m2+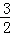 m��
m��
��S��PAC=S��PAQ+S��PCQ=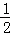 ������
������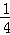 m2+
m2+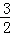 m����6
m����6
=��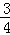 ��m��3��2+
��m��3��2+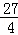 ��
��
�൱m=3ʱ����PAC��������Ϊ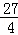 ��
��
��ʱ��P�������Ϊ��3��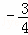 ������10�֣�
������10�֣�





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����˵����ȷ���ǣ�������
| �� | A�� | Ϊ���˽�ȫ����ѧ��ÿ������������ʱ�䣬Ӧ�����ղ�ķ�ʽ |
| �� | B�� | ���������ݵķ���S |
| �� | C�� | �㰲������һ�������� |
| �� | D�� | һ������4��5��6��5��2��8��������5 |


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ1��ʾ�����¼ܣ�֧������ͼ�Ļ���ͼ�������Σ���ʾ��ͼ��ͼ2.���¼�����ʱ���� ������
������ 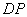 �ϻ�������
�ϻ�������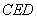 �Ĵ�СҲ��֮�����仯.��֪ÿ�����α߳�������20cm ,��
�Ĵ�СҲ��֮�����仯.��֪ÿ�����α߳�������20cm ,��
 =20cm .
=20cm .
�� ����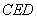 =60��ʱ����
=60��ʱ����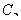
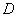 �����ľ��룻
�����ľ��룻
�� ����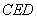 ��60���Ϊ120��ʱ����
��60���Ϊ120��ʱ����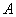 �����ƶ��˶���cm ?(�����ȷ��0.1cm)
�����ƶ��˶���cm ?(�����ȷ��0.1cm)
�� ��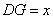 cm ,����
cm ,����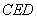 �ı仯��ΧΪ60��~ 120��(�����˵�ֵ)ʱ����
�ı仯��ΧΪ60��~ 120��(�����˵�ֵ)ʱ����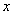 ��ȡֵ��Χ .(�����ȷ��0.1cm) (�ο�����
��ȡֵ��Χ .(�����ȷ��0.1cm) (�ο�����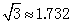 ����ʹ�ÿ�ѧ������)
����ʹ�ÿ�ѧ������)


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

 ��ȫ��������ѧ�����У���������40��ͬѧ���븴���������ǵijɼ���Ϊ���飬��һ��һ������������ֱ�Ϊ10��5��7��6���������Ƶ����0.2����������Ƶ������
��ȫ��������ѧ�����У���������40��ͬѧ���븴���������ǵijɼ���Ϊ���飬��һ��һ������������ֱ�Ϊ10��5��7��6���������Ƶ����0.2����������Ƶ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
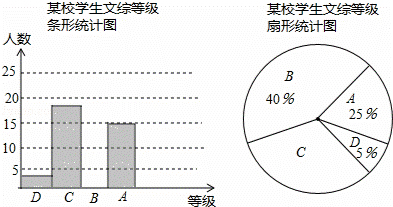
�����Ǿ��꼶ij��ѧ����Ӧ�Կ������۳ɼ�������A��B��C��D�ȼ����֣���A��Ϊ�ɼ���ã�������ͳ��ͼ������ͳ��ͼ�������ͼ�е���Ϣ�ش��������⣺����
��1����ȫ����ͳ��ͼ��
��2����C������Ӧ������ͳ��ͼ��Բ�ĽǵĶ�����
��3����ð�ѧ�����ж����ˣ�
��4��������۳ɼ���B�ȼ�B�����ϵ�ѧ�����ܱ���ʾ���Ը��У������øð�ѧ����������Ƹ�У���꼶400��ѧ���У��ж�����ѧ�����ʸ�ʾ���Ը��У�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪��A��˫����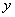
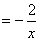 �ϣ���B��ֱ��
�ϣ���B��ֱ��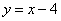 �ϣ���A��B�������
�ϣ���A��B�������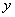 ��Գƣ����A������Ϊ��
��Գƣ����A������Ϊ��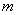 ��
��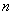 ������
������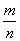 +
+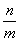 ��ֵ�� ( )
��ֵ�� ( )
��A��-10 ��B��-8 ��C��6 ��D��4


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����5��10�գ�����ί���������н����ֵȵ�λ���Ͼٰ�ġ��߸���·��Բ�й��Ρ���ѧ���ݽ������У�7λ��ί������ѡ������ͬѧ�Ĵ�������
| ������ | A | B | C | D | E | F | G |
| ���� | 90 | 92 | 86 | 92 | 90 | 95 | 92 |
������ͬѧ�÷ֵ�����Ϊ��������
| �� | A�� | 95 | B�� | 92 | C�� | 90 | D�� | 86 |


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
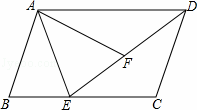
��ͼ����ƽ���ı���ABCD�У���B=��AFE��EA�ǡ�BEF�Ľ�ƽ���ߣ���֤��
��1����ABE�ա�AFE��
��2����FAD=��CDE��


�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com