
����Ŀ��ijУΪѡ��һ��ѡ�ֲμ����������ţ���Ϊ�����������������ݽ����������о�������ͼ��ʾ����Ŀ��Ȩ����ѡ��������ѡ�ֽ��п��������Ű�ԭ��ͳ��ͼ�����������±����������Ż���ѡ�����еĵ÷������

��װ | ��ͨ�� | ���� | �ݽ����� | |
���� | 85 | 70 | 80 | 85 |
�Ż� | 90 | 75 | 75 | 80 |
���������Ϣ���ش��������⣺
��1�����װ��Ŀ��ѡ�ֿ����е�Ȩ����
��2����������ѧ��֪ʶ������ѧУ���������Ż�������ѡ��һ�˲μ����������ţ���Ϊ�����������������ݽ���������˵�����ɣ�
���𰸡���1����װ�ڿ����е�Ȩ��Ϊ10%����2��ѡ�������μӱ������������������ܳɼ��ߣ�
��������
��1��������Ŀ��ռ����Ȩ��Ϊ100%����100%�м�ȥ����������Ŀ��Ȩ�����ɣ�
��2�������������Ż����ܳɼ�������Ȩƽ�����Ƚϵó��𰸣�
��1����װ�ڿ����е�Ȩ��Ϊ��1-20%-30%-40%=10%��
�𣺷�װ�ڿ����е�Ȩ��Ϊ10%��
��2��ѡ�������μӱ�����
�������ܳɼ�Ϊ��85��10%+70��20%+80��30%+85��40%=80.5�֣�
�Ż��ijɼ�Ϊ��90��10%+75��20%+75��30%+80��40%=78.5�֣�
��Ϊ80.5��78.5��
���������ɼ��Ϻã�ѡ�������ɼ�������
��ѡ�������μӱ������������������ܳɼ��ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF����GAC��
��1����֤����ADE�ס�ABC��
��2����AD��BE��4��AE��3����CD��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
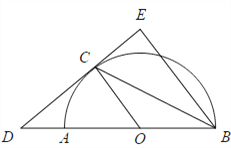
����Ŀ����ͼ����֪![]() ��
��![]() ��ֱ����CD��
��ֱ����CD��![]() ������C��
������C�� ![]() .
.
��1����֤��BC ��![]() ��ƽ����.
��ƽ����.
��2����DC=8�� ![]() �İ뾶OA=6����CE�ij�.
�İ뾶OA=6����CE�ij�.
���𰸡���1��֤������������2��4.8
����������������1����![]() ���Ƴ�
���Ƴ�![]() ����
����![]() ���Ƴ�
���Ƴ�![]() ���ɵ�
���ɵ�![]() .��2����
.��2����![]() �����OD����
�У����OD����![]() ���ɵ�
���ɵ�![]() ���ɴ˼��ɽ������.
���ɴ˼��ɽ������.
��⣺��1��֤������Ϊ![]() ��
��
����![]() ��
��
����Ϊ![]() ��
��
����![]() ��
��
�ʿɵ�![]() ��
��
���ɵ�![]() ��
��![]() ��ƽ����.
��ƽ����.
��2����ΪDE��![]() �����ߣ�
�����ߣ�
����![]() ������
������![]() ��DC=8��OC=OA=6,����
��DC=8��OC=OA=6,����![]() ��
��
����Ϊ![]() ��
��
����![]() ��
��
����![]() ��
��
���ɵ�EC=4.8
�㾦��������Ҫ���������ߵ����ʼ����������ε�Ӧ�ã���Ŀ�Ѷ����У����ۺ������������֪ʶ���ǽ���Ĺؼ�.
�����͡������
��������
23
����Ŀ����ʳƷ��ȫ���ܵ�ȫ���Ĺ㷺��ע��������ij��ѧ�Բ���ѧ����ʳƷ��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ�����������.
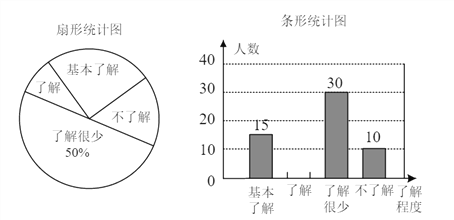
��1�������ʾ������ѧ������_____�ˣ�����ͳ��ͼ���������˽�����������Ӧ���ε�Բ�Ľ�Ϊ_____.
��2���벹ȫ����ͳ��ͼ.
��3��������ѧ����ѧ��900�ˣ���������������������Ƹ���ѧѧ���ж�ʳƷ��ȫ֪ʶ�ﵽ���˽������������˽����̶ȵ�������.
��4�����Ӷ�ʳƷ��ȫ֪ʶ�ﵽ���˽����̶ȵ�2��Ů����2�������������ȡ2�˲μ�ʳƷ��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽1��������1��Ů���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȥ�Ϸ�������Ҷ����ij��A�����г���ÿ��mԪ�ļ۸����40����Ҷ���ֵ�B�����г�ʱ����ͬ���IJ�Ҷ��A�����г�Ҫ���ˣ�ÿ���ļ۸��ΪnԪ�����������B�����г�����60��ͬ���IJ�Ҷ�����������ʱ��ÿ��![]() Ԫ�ļ۸�ȫ������������Ҷ����ô�ڲ������������ص�������������������������
Ԫ�ļ۸�ȫ������������Ҷ����ô�ڲ������������ص�������������������������
A.һ��ӯ��B.һ������
C.��ӯ����D.ӯ������ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������
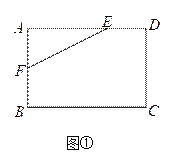
��1����ͼ�٣��ھ���ABCD�У�AB=4��AD=6��AE=4��AF=2���Ƿ��ڱ�BC��CD�Ϸֱ���ڵ�G��H��ʹ���ı���EFGH���ܳ���С�������ڣ�������ܳ�����Сֵ���������ڣ���˵�����ɣ�
��������
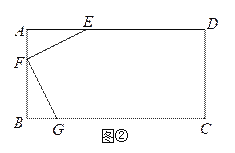
��2����ͼ�ڣ���һ���ΰ��ABCD��AB=3�ף�AD=6�ף�����Ӵ˰���вó�һ����������ܴ���ı���EFGH������ʹ��EFG=90����EF=FG=![]() �ף���EHG=45�������о���ֻ�е���E��F��G�ֱ��ڱ�AD��AB��BC�ϣ���AF��BF���������H�ھ���ABCD�ڲ������ʱ�����п��ܲó�����Ҫ��IJ����������ܷ�õ÷���Ҫ�����������ܴ���ı���EFGH���������ܣ�����õõ��ı���EFGH�������������д������BΪ����ԭ�㣬ֱ��BCΪx�ᣬֱ��BAΪy�������ϵ�У���H�����ꣻ�����ܣ���˵�����ɣ�
�ף���EHG=45�������о���ֻ�е���E��F��G�ֱ��ڱ�AD��AB��BC�ϣ���AF��BF���������H�ھ���ABCD�ڲ������ʱ�����п��ܲó�����Ҫ��IJ����������ܷ�õ÷���Ҫ�����������ܴ���ı���EFGH���������ܣ�����õõ��ı���EFGH�������������д������BΪ����ԭ�㣬ֱ��BCΪx�ᣬֱ��BAΪy�������ϵ�У���H�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
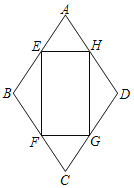
����Ŀ����ͼ������ABCD�У�AB=1����A=60����EFGH�Ǿ��Σ����εĶ��㶼�����εı��ϣ���AE=AH=x��0��x��1�������ε����ΪS��
��1����S����x�ĺ�������ʽ��
��2����EFGH��������ʱ����S��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵ�A��Ӧ�����ǩ�1��B���Ӧ������1��һֻС��״ӵ�B���������������������ÿ��4����λ���ٶ�������C�㣬���������ص�A�㣬������4���ӣ�
��1�����C��Ӧ������
��2����С����ص�A������������˶�����1����������2����λ����2����������4����λ����3����������6����λ����4����������8����λ�������ι�������ȥ��������10��������ͣ�ڵ�����Ӧ������
��3����С����ص�A�������������ĸ�������ÿ��4����λ���ٶ����У���ʱ��һС���Ҵӵ�C������������ĸ�������ÿ��7����λ���ٶ����У����С���Ӧ�ĵ�ΪE�㣬��С���Ӧ�ĵ�ΪF�㣬���A��E��F��B����Ӧ�����ֱ���xA��xE��xF��xB�����˶�ʱ��t������1��ʱ��������������� |xA��xE |��|xE��xF |+ |xF��xB |= .(ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AE��CF�ֱ�ֱ��EF��AC���أ���֪����1=��2��ABƽ����EAC��CDƽ����ACG��������֤��AB��CD�Ĺ��̼�������д������
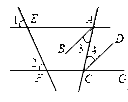
֤������ ��1="��2" �� ��֪ ��
�� AE�� �� ��
�� ��EAC =�� ���� ��
��ABƽ����EAC��CDƽ����ACG�� ��֪ ��
��� =![]() ��EAC����4=
��EAC����4=![]() �� �� ��ƽ���ߵĶ��� ��
�� �� ��ƽ���ߵĶ��� ��
��� =��4������������
��AB��CD�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
�У�![]() ,
,![]() ,
,![]() ,
,![]() ������
������![]() ,��
,��![]() �����ı���
�����ı���![]() ���ϵ�һ�㣻����
���ϵ�һ�㣻����![]() ��
��![]() �ľ���Ϊ
�ľ���Ϊ![]() �������ĵ�
�������ĵ�![]() �� �� ��
�� �� ��
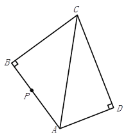
A. 0��B. 1��C. 2��D. 3��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com