
嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2++bx+c=0变形为:
x2+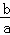 x=﹣
x=﹣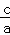 ,…第一步
,…第一步
x2+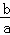 x+(
x+( )2=﹣
)2=﹣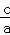 +(
+( )2,…第二步
)2,…第二步
(x+ )2=
)2=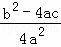 ,…第三步
,…第三步
x+ =
=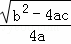 (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步
x= ,…第五步
,…第五步
嘉淇的解法从第 四 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 x=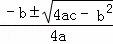 .
.
用配方法解方程:x2﹣2x﹣24=0.
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
某种正方形合金板材的成本y(元)与它的面积成正比,设边长为x厘米.当x=3时,y=18,那么当成本为72元时,边长为( )
|
| A. | 6厘米 | B. | 12厘米 | C. | 24厘米 | D. | 36厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
五名学生投篮球,规定每人投20次,统计他们每人投中的次数.得到五个数据.若这五个数据的中位数是6.唯一众数是7,则他们投中次数的总和可能是( )
|
| A. | 20 | B. | 28 | C. | 30 | D. | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某景区内的环形路是边长为800米的正方形ABCD,如图1和图2.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
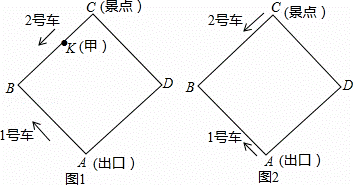
探究:设行驶吋间为t分.
(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y1,y2(米) 与t(分)的函数关系式,并求出当两车相距的路程是400米时t的值;
(2)t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇过的次数.
发现:如图2,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A,设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多?(含候车时间)
决策:己知游客乙在DA上从D向出口A走去.步行的速度是50米/分.当行进到DA上一点P (不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由:
(2)设PA=s(0<s<800)米.若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中.他该如何选择?
查看答案和解析>>
科目:初中数学 来源: 题型:
下列调查中,适合用全面调查的是( )
A 了解某班同学立定跳远的情况 B 了解一批炮弹的杀伤半径
C 了解某种品牌奶粉中含三聚氰胺的百分比 D 了解全国青少年喜欢的电视节目
查看答案和解析>>
科目:初中数学 来源: 题型:
在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白
板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低
于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com