
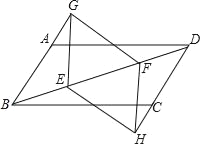
【题目】如图,在ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:(1)△BEG≌△DFH;
(2)四边形GEHF是平行四边形.
科目:初中数学 来源: 题型:
【题目】将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有245个“○”,则n=( )

A. 14 B. 15 C. 16 D. 17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ).

A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图,点A、B在数轴上分别表示有理数a、b,则A、B两点之间的距离可以表示为|a﹣b|.
根据阅读材料与你的理解回答下列问题:
(1)数轴上表示3与﹣2的两点之间的距离是 .
(2)数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为 .
(3)代数式|x+8|可以表示数轴上有理数x与有理数 所对应的两点之间的距离;若|x+8|=5,则x= .
(4)求代数式|x+1008|+|x+504|+|x﹣1007|的最小值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN.
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林同学积极参加体育锻炼,天天坚持跑步,他每天以1000m为标准,超过的记作正数,不足的记作负数.下表是一周内小明跑步情况的记录(单位:m):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
跑步情况(m) | +420 | +460 | -100 | -210 | -330 | +200 | -240 |
(1)星期三小林跑了_____米
(2)小林在跑得最少的一天跑了______米?跑得最多的一天比最少的一天多跑了_____米?
(3)若小林跑步的平均速度为240米/分,求本周内小明用于跑步的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
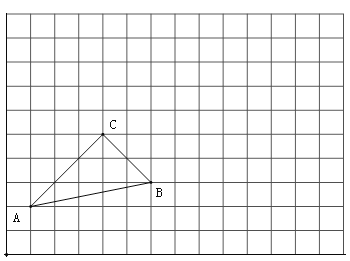
【题目】如图,△ABC是格点三角形(各顶点是网格线的交点), 每个小方格都是边长为1个单位长度的小正方形.
(1)将△ABC向右平移6个单位长度,画出平移后的△A1B1C1.
(2)将平移后的△A1B1C1绕点B1顺时针旋转90°,画出旋转后的△A2B1C2.
(3)将△ABC沿直线BC翻折,画出翻折后的△A3BC.
(4)试问△ABC能否经过一次旋转后与△A2B1C2重合,若能,请在图中用字母O表示旋转中心并写出旋转角的大小;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2﹣(m+n)x+n(m<0)的图象与y轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当﹣3<p<0时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com