
【题目】八年 2 班组织了一次经典诵读比赛,甲乙两组各 10 人的比赛成绩如下表(10 分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(Ⅰ)甲组数据的中位数是 ,乙组数据的众数是 ;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是 1.4 分,则成绩较为整齐的是 。
【答案】(1)9.5,10;(2)9,1;(3)乙组.
【解析】
(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可; (2)先求出乙组的平均成绩,再根据方差公式进行计算; (3)先比较出甲组和乙组的方差,再根据方差的意义即可得出答案.
解:(1)把甲组的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,
最中间两个数的平均数是(9+10)÷2=9.5(分),则中位数是9.5分;
乙组成绩中10出现了4次,出现的次数最多,则乙组成绩的众数是10分; 故答案为:9.5,10;
(2)乙组的平均成绩是:![]() (10×4+8×2+7+9×3)=9,
(10×4+8×2+7+9×3)=9,
则方差是:![]() [4×(10-9)2+2×(8-9)2+(7-9)2+3×(9-9)2]=1;
[4×(10-9)2+2×(8-9)2+(7-9)2+3×(9-9)2]=1;
(3)∵甲组成绩的方差是1.4,乙组成绩的方差是1,
∴成绩较为整齐的是乙组,故答案为乙组.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,萧山区大力发展旅游业,跨湖桥遗址、湘湖二期三期、宋城千古情、河上民俗、大美进化……这些名词,相信同学们都耳熟能详了,因此近年来,我区的年游客接待量呈逐年稳步上升,2015年接待1800万人次,2015——2017年这三年累计接待游客高达5958万人次.
(1)求萧山区2015——2017年年游客接待量的年平均增长率.
(2)若继续呈该趋势增长,请预测2018年年游客接待量(近似到万人次).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲得分的方差比乙得分的方差小B. 甲得分的众数是8,乙得分的众数是9
C. 甲、乙得分的平均数都是8D. 甲得分的中位数是9,乙得分的中位数是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AD 与 BC 相交于 E ,1 2 3, BD CD, ADB 90, CH AB于 H , CH 交 AD 于 F 。
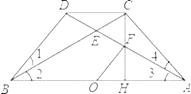
(1)求证: CD∥ AB ;
(2)求证: BDE ≌ ACE ;
(3)若O 为 AB 中点,求证:OF=![]() BE 。
BE 。
查看答案和解析>>
科目:初中数学 来源: 题型:
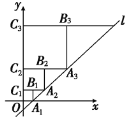
【题目】如图:在平面直角坐标系中,直线l:![]() 与x轴交于点A1,如图所示依次作正方形A1B1C1O、
与x轴交于点A1,如图所示依次作正方形A1B1C1O、
正方形A2B2C2C1、…、正方形![]() ,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…
,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…
在y轴正半轴上,则点![]() 的坐标是_______________________.
的坐标是_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
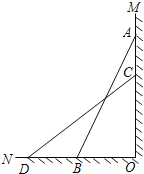
【题目】某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4 m吗?为什么?
(3)亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,会思考问题的你能说出这个点并说明其中的道理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A. B在双曲线y=![]() (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
(x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
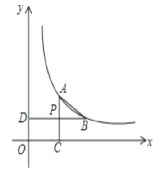
(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com