
【题目】已知:正方形![]() 的边长为
的边长为![]() 厘米,对角线
厘米,对角线![]() 上的两个动点
上的两个动点![]() ,
,![]() .点
.点![]() 从点
从点![]() ,点
,点![]() 从点
从点![]() 同时出发,沿对角线以
同时出发,沿对角线以![]() 厘米/秒的相同速度运动,过
厘米/秒的相同速度运动,过![]() 作
作![]() 交
交![]() 的直角边于
的直角边于![]() ,过
,过![]() 作
作![]() 交
交![]() 的直角边于
的直角边于![]() ,连接
,连接![]() ,
,![]() .设
.设![]() 、
、![]() 、
、![]() 、
、![]() 围成的图形面积为
围成的图形面积为![]() ,
,![]() ,
,![]() ,
,![]() 围成的图形面积为
围成的图形面积为![]() (这里规定:线段的面积为
(这里规定:线段的面积为![]() 到达
到达![]() ,
,![]() 到达
到达![]() 停止.若
停止.若![]() 的运动时间为
的运动时间为![]() 秒,解答下列问题:
秒,解答下列问题:

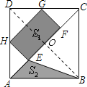
![]() 如图,判断四边形
如图,判断四边形![]() 是什么四边形,并证明;
是什么四边形,并证明;
![]() 当
当![]() 时,求
时,求![]() 为何值时,
为何值时,![]() ;
;
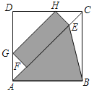
![]() 若
若![]() 是
是![]() 与
与![]() 的和,试用
的和,试用![]() 的代数式表示
的代数式表示![]() .(如图为备用图)
.(如图为备用图)
【答案】![]() 四边形
四边形![]() 是矩形,理由见解析;
是矩形,理由见解析;![]() 当
当![]() 时,
时,![]() ;
;![]() .
.
【解析】
(1)根据题意可得AE=CF=x,再证明四边形![]() 是平行四边形,根据有一个角是直角的平行四边形是矩形即可证得结论;(2)由勾股定理求出正方形ABCD的对角线长为16.连接BD交AC于O,可得BO=8.用含x的代数式分别表示S1、 S2,当S1=S2时得出关于x的方程,解方程即可求解;(3)分0≤x<8与8≤x≤16两种情况求解即可.
是平行四边形,根据有一个角是直角的平行四边形是矩形即可证得结论;(2)由勾股定理求出正方形ABCD的对角线长为16.连接BD交AC于O,可得BO=8.用含x的代数式分别表示S1、 S2,当S1=S2时得出关于x的方程,解方程即可求解;(3)分0≤x<8与8≤x≤16两种情况求解即可.
![]() 四边形
四边形![]() 是矩形.理由如下:
是矩形.理由如下:
∵点![]() 从点
从点![]() ,点
,点![]() 从点
从点![]() 同时出发,沿对角线以
同时出发,沿对角线以![]() 厘米/秒的相同速度运动,
厘米/秒的相同速度运动,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 为正方形,
为正方形,
∴![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵![]()
∴平行四边形![]() 是矩形;
是矩形;
![]() ∵正方形边长为
∵正方形边长为![]() ,
,
∴![]() .
.
∵![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,则
,则![]() 且
且![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() ,
,
解得![]() (舍去),
(舍去),![]() .
.
∴当![]() 时,
时,![]() ;
;
![]() ①当
①当![]() 时,
时,![]() .
.
②当![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
综上,可知![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩,测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
(1)小明将三人的成绩整理后制作了下面的表格:
平均数 | 中位数 | 众数 | 方差 | |
甲 | 7 | b | 7 | 0.8 |
乙 | 7 | 7 | d | 0.4 |
丙 | a | c | e | 0.81 |
则表中a= ,b= ,c= ,d= ,e= .
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请作出简要分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,解一元一次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想,我们还可以解一些新的方程,例如一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)用“转化”思想求方程![]() =x的解.
=x的解.
(3)如图,已知矩形草坪ABCD的长AD=14m,宽AB=12m,小华把一根长为28m的绳子的一端固定在点B处,沿草坪边沿BA、AD走到点P处,把长绳PB段拉直并固定在点P处,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C处,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角△ABC中,∠BAC=90°,AB=3,M是边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好在边AC的中点处,那么点M到AC的距离是( )

A. 1.5 B. 2 C. 2.5 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
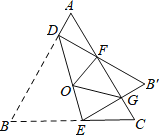
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的解析式是![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 抛物线的对称轴是直线![]() B. 抛物线的顶点坐标是
B. 抛物线的顶点坐标是![]() C. 该二次函数有最小值
C. 该二次函数有最小值![]() D. 当
D. 当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com