2.【课本节选】
反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线.当k>0时,双曲线两个分支分别在一、三象限,在每一个象限内,y随x的增大而减小(简称增减性);反比例函数的图象关于原点对称(简称对称性).
这些我们熟悉的性质,可以通过说理得到吗?
【尝试说理】
我们首先对反比例函数y=$\frac{k}{x}$(k>0)的增减性来进行说理.
如图,当x>0时.
在函数图象上任意取两点A、B,设A(x
1,$\frac{k}{{x}_{1}}$),B(x
2,$\frac{k}{{x}_{2}}$),
且0<x
1<x
2.
下面只需要比较$\frac{k}{{x}_{1}}$和$\frac{k}{{x}_{2}}$的大小.
$\frac{k}{{x}_{2}}$-$\frac{k}{{x}_{1}}$=$\frac{k({x}_{1}-{x}_{2})}{{{x}_{1}x}_{2}}$
∵0<x
1<x
2,∴x
1-x
2<0,x
1x
2>0,且 k>0.
∴$\frac{k({x}_{1}-{x}_{2})}{{{x}_{1}x}_{2}}$<0.即$\frac{k}{x_2}$<$\frac{k}{x_1}$.
这说明:x
1<x
2时,$\frac{k}{{x}_{1}}$>$\frac{k}{{x}_{2}}$.也就是:自变量值增大了,对应的函数值反而变小了.
即:当x>0时,y随x的增大而减小.同理,当x<0时,y随x的增大而减小.
(1)试说明:反比例函数y=$\frac{k}{x}$ (k>0)的图象关于原点对称.
【运用推广】
(2)分别写出二次函数y=ax
2 (a>0,a为常数)的对称性和增减性,并进行说理.
对称性:二次函数y=ax
2(a>0,a为常数)的图象关于y轴成轴对称;
增减性:当x>0时,y随x增大而增大;当x<0时,y随x增大而减小..
说理:①∵在二次函数y=ax
2(a>0,a为常数)的图象上任取一点Q(m,n),于是n=am
2.
∴点Q关于y轴的对称点Q
1(-m,n).
而n=a(-m)
2,即n=am
2.
这说明点Q
1也必在在二次函数y=ax
2(a>0,a为常数)的图象上.
∴二次函数y=ax
2(a>0,a为常数)的图象关于y轴成轴对称;
②在二次函数y=ax
2(a>0,a为常数)的图象上任取两点A、B,
设A(m,am
2),B(n,an
2),且0<m<n.
则an
2-am
2=a(n+m)(n-m),
∵n>m>0,
∴n+m>0,n-m>0;
∵a>0,
∴an
2-am
2=a(n+m)(n-m)>0,即an
2>am
2.
而当m<n<0时,n+m<0,n-m>0;
∵a>0,
∴an
2-am
2=a(n+m)(n-m)<0.即an
2<am
2.
这说明,当x>0时,y随x增大而增大;当x<0时,y随x增大而减小;.
【学以致用】
(3)对于函数y=x
2+$\frac{2}{x}$ (x>0),
请你从增减性的角度,请解释为何当x=1时函数取得最小值.
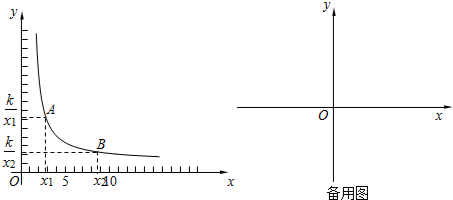

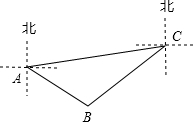 如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)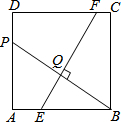 如图,在边长为8的正方形ABCD中,P为AD上一点,且AP=5,BP的垂直平分线分别交AB、DC于E、F,点Q为垂足,则线段EQ:QF的值是$\frac{5}{11}$.
如图,在边长为8的正方形ABCD中,P为AD上一点,且AP=5,BP的垂直平分线分别交AB、DC于E、F,点Q为垂足,则线段EQ:QF的值是$\frac{5}{11}$.