
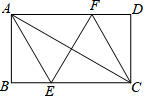
 如图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF,若AB=2$\sqrt{3}$,∠DCF=30°,则EF的长为( )
如图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF,若AB=2$\sqrt{3}$,∠DCF=30°,则EF的长为( )| A. | 4 | B. | 6 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 求出∠ACB=∠DAC,然后利用“角角边”证明△AOF和△COE全等,根据全等三角形对应边相等可得OE=OF,再根据对角线互相垂直平分的四边形是菱形得到四边形AECF是菱形,再求出∠ECF=60°,然后判断出△CEF是等边三角形,根据等边三角形的三条边都相等可得EF=CF,根据矩形的对边相等可得CD=AB,然后求出CF,从而得解.
解答 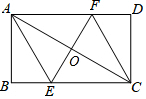 解:∵矩形对边AD∥BC,
解:∵矩形对边AD∥BC,
∴∠ACB=∠DAC,
∵O是AC的中点,
∴AO=CO,
在△AOF和△COE中,
$\left\{\begin{array}{l}{∠FAO=∠OCE}\\{AO=CO}\\{∠AOF=∠EOC}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴OE=OF,
又∵EF⊥AC,
∴四边形AECF是菱形,
∵∠DCF=30°,
∴∠ECF=90°-30°=60°,
∴△CEF是等边三角形,
∴EF=CF,
∵AB=2$\sqrt{3}$,
∴CD=AB=2$\sqrt{3}$,
∵∠DCF=30°,
∴CF=2$\sqrt{3}$÷$\frac{\sqrt{3}}{2}$=4,
∴EF=4,
故选:A.
点评 本题考查了菱形的判定与性质,矩形的性质,全等三角形的判定与性质,等边三角形的判定与性质,难点在于判断出△CEF是等边三角形.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$,1 | B. | -$\frac{5}{3}$,1 | C. | $\frac{5}{3}$,2 | D. | -$\frac{5}{3}$,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
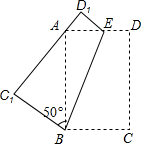 如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,BC是⊙O的直径,A是CB延长线上一点,AD切⊙O于点D,如果AB=2,∠A=30°,那么⊙O半径等于( )
如图,BC是⊙O的直径,A是CB延长线上一点,AD切⊙O于点D,如果AB=2,∠A=30°,那么⊙O半径等于( )| A. | 2 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
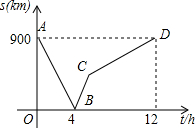 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为t(h),两车之间的距离为s(km),图中的折线表示s与t之间的函数关系,根据图象提供的信息有下列说法:①甲、乙两地之间的距离为900km; ②行驶4h两车相遇; ③快车的速度为150km/h; ④行驶6h两车相距450km; ⑤相遇时慢车行驶了280km; ⑥行驶6h快车停止了行驶.其中符合图象描述的说法有( )个.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为t(h),两车之间的距离为s(km),图中的折线表示s与t之间的函数关系,根据图象提供的信息有下列说法:①甲、乙两地之间的距离为900km; ②行驶4h两车相遇; ③快车的速度为150km/h; ④行驶6h两车相距450km; ⑤相遇时慢车行驶了280km; ⑥行驶6h快车停止了行驶.其中符合图象描述的说法有( )个.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -3 | C. | -$\frac{5}{3}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com