Question

7．已知直角坐标系中菱形ABCD中的位置如图，C、D两点的坐标分别为（4，0），（0，3）．现有两动点P、Q分别从A、C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，P运动到D时整个运动停止，设运动时间为t秒．
（1）填空：菱形ABCD的边长5、面积是24、高BE的长是$\frac{24}{5}$；
（2）若点P的速度为每秒1个单位长度，点Q的速度为每秒2个单位长度．当点Q在线段BA上时，求△APQ的面积S关于t的函数解析式及定义域；
（3）若点P的速度为每秒1个单位长度，点Q的速度为每秒k个单位长度（0＜k≤2）．当t=4秒时，△APQ恰好是一个等腰三角形，求k的值．

Answer 1

分析 （1）求出OC=4，OD=3，在Rt△COD中，由勾股定理求出CD=5，求出AC=2OC=8，BD=2OD=6，即可求出菱形ABCD的面积（$\frac{1}{2}$×AC×BD），根据S=AD×BE，求出BE即可；
（2）求出AP=t，AQ=10-2t，过点Q作QG⊥AD，垂足为G，根据△AQG∽△ABE求出QG=$\frac{48}{5}$-$\frac{48}{25}$t，代入S=$\frac{1}{2}$AP•QG求出即可；
（3）当t=4秒时，求出AP=4，分两种情况讨论：①当点Q在CB上时，只有Q₁A=Q₁P，过点Q₁作Q₁M⊥AP，垂足为点M，Q₁M交AC于点F，根据△AMF∽△AOD∽△CQ₁F求出FM=$\frac{3}{2}$，Q₁F=$\frac{33}{10}$，CQ₁=$\frac{4}{3}$QF=$\frac{22}{5}$，由CQ₁=4k，求出即可；②当点Q在BA上时，存在两点Q₂，Q₃，分别使AP=AQ₂，PA=PQ₃．
Ⅰ、若AP=AQ₂，根据CB+BQ₂=10-4=6得出4k=6，求出即可；
Ⅱ、若PA=PQ₃，过点P作PN⊥AB，垂足为N，由△ANP∽△AEB，得$\frac{AN}{AE}=\frac{AP}{AB}$，求出AN=$\frac{28}{25}$，AQ₃=2AN=$\frac{56}{25}$，求出BC+BQ₃=$\frac{194}{25}$，由4k=$\frac{194}{25}$，求出即可

解答 解：（1）∵C，D两点的坐标分别为（4，0），（0，3），
∴OC=4，OD=3，
在Rt△COD中，由勾股定理得：CD=5，
即菱形ABCD的边长是5，
∵四边形ABCD是菱形，
∴AD=DC=5，AC⊥BD，AC=2OC=8，BD=2OD=6，
∴菱形ABCD的面积是$\frac{1}{2}$×AC×BD=$\frac{1}{2}$×8×6=24，
∴24=AD×BE，
∴BE=$\frac{24}{5}$；
故答案为：5，24，$\frac{24}{5}$．

（2）由题意，得AP=t，AQ=10-2t，
如图1，过点Q作QG⊥AD，垂足为G，由QG∥BE得：
△AQG∽△ABE，
∴$\frac{QG}{BE}=\frac{QA}{AB}$，
∴QG=$\frac{48}{5}-\frac{48}{25}$t，
∴S=$\frac{1}{2}$AP•QG=$\frac{1}{2}$•t•（$\frac{48}{5}$-$\frac{48}{25}$t），
S=-$\frac{24}{25}$t²+$\frac{24}{5}$t（$\frac{5}{2}$≤t≤5）；

（3）当t=4秒时，
∵点P的速度为每秒1个单位，
∴AP=4，
①当点Q在CB上时，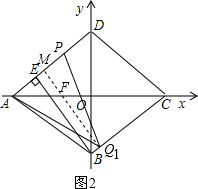
∵PQ≥BE＞PA，
∴只存在点Q₁，使Q₁A=Q₁P，
如图2，过点Q₁作Q₁M⊥AP，垂足为点M，Q₁M交AC于点F，
则AM=$\frac{1}{2}$AP=2，
∵△AMF∽△AOD∽△CQ₁F，
∴$\frac{FM}{AM}=\frac{F{Q}_{1}}{C{Q}_{1}}=\frac{OD}{AO}$=$\frac{3}{4}$，
∴FM=$\frac{3}{2}$，
∴Q₁F=MQ₁-FM=$\frac{33}{10}$，
∴CQ₁=$\frac{4}{3}$QF=$\frac{22}{5}$，
由CQ₁=4k，
∴k=$\frac{11}{10}$；
②当点Q在BA上时，存在两点Q₂，Q₃，分别使AP=AQ₂，PA=PQ₃．
Ⅰ、若AP=AQ₂，如图3，
CB+BQ₂=10-4=6．由4k=6，得k=$\frac{3}{2}$；
Ⅱ、若PA=PQ₃，如图4，
过点P作PN⊥AB，垂足为N，
由△ANP∽△AEB，得$\frac{AN}{AE}=\frac{AP}{AB}$，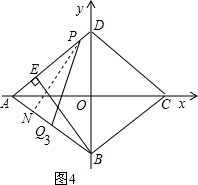
∵AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\frac{7}{5}$，
∴AN=$\frac{28}{25}$，
∴AQ₃=2AN=$\frac{56}{25}$，
∴BC+BQ₃=10-$\frac{56}{25}$=$\frac{194}{25}$，由4k=$\frac{194}{25}$，
得k=$\frac{97}{50}$．
综上所述，当t=4秒，使得△APQ为等腰三角形的k的值为$\frac{11}{10}$或$\frac{3}{2}$或$\frac{97}{50}$．

点评 此题是四边形综合题，主要考查了相似三角形的性质和判定，勾股定理，菱形性质的应用，查学生综合运用性质进行推理和计算的能力，难度偏大，分类讨论思想是解本题的难点．