
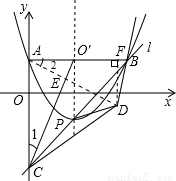
 x2-2x+1的顶点为P,A为抛物线与y轴的交点,过A与y轴垂直的直线与抛物线的另一交点为B,与抛物线对称轴交于点O′,过点B和P的直线l交y轴于点C,连接O′C,将△ACO′沿O′C翻折后,点A落在点D的位置.
x2-2x+1的顶点为P,A为抛物线与y轴的交点,过A与y轴垂直的直线与抛物线的另一交点为B,与抛物线对称轴交于点O′,过点B和P的直线l交y轴于点C,连接O′C,将△ACO′沿O′C翻折后,点A落在点D的位置.
 x-
x- .根据题意还可求得,抛物线上存在两点Q1(2,-1)(即点P)和Q2(
.根据题意还可求得,抛物线上存在两点Q1(2,-1)(即点P)和Q2( ,
, ),使得S△DQC=S△DPB.
),使得S△DQC=S△DPB. (x-2)2-1,
(x-2)2-1, x2-2x+1,
x2-2x+1, ,
,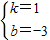 ∴
∴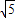 .
. ×O′C×AE=
×O′C×AE= ×O′A×CA,
×O′A×CA, ,AD=2AE=
,AD=2AE= .
.
 ,
, •AC=
•AC=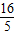 ,DF=
,DF= •O′A=
•O′A= ,(5分)
,(5分) =-
=- ,
,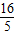 ,-
,- ).(6分)
).(6分)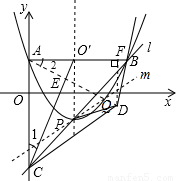
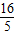 ,-
,- )的直线的解析式为y=
)的直线的解析式为y= x-3,
x-3, x-
x- .
. x2-2x+1=
x2-2x+1= x-
x- ,
, ,
, x-
x- ,得y1=-1,y2=
,得y1=-1,y2= ,
, ,
, ),使得S△DQC=S△DPB.(9分)
),使得S△DQC=S△DPB.(9分)

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
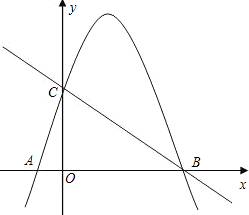 C(0,3).
C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:
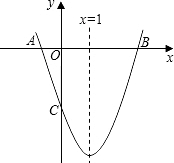 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.查看答案和解析>>
科目:初中数学 来源: 题型:
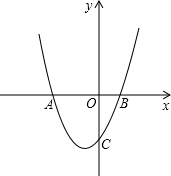 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com