
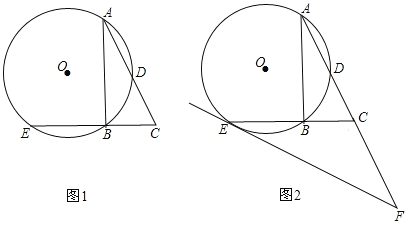
ЁОЬтФПЁП(2016ЫФДЈЪЁРжЩНЪаЕк25Ьт)вбжЊRtЁїABCжаЃЌABЪЧЁбOЕФЯвЃЌаББпACНЛЁбOгкЕуDЃЌЧвAD=DCЃЌбгГЄCBНЛЁбOгкЕуEЃЎ
ЃЈ1ЃЉЭМ1ЕФAЁЂBЁЂCЁЂDЁЂEЮхИіЕужаЃЌЪЧЗёДцдкФГСНЕуМфЕФОрРыЕШгкЯпЖЮCEЕФГЄЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуEзїЁбOЕФЧаЯпЃЌНЛACЕФбгГЄЯпгкЕуFЃЎ
ЂйШєCF=CDЪБЃЌЧѓsinЁЯCABЕФжЕЃЛ
ЂкШєCF=aCDЃЈaЃО0ЃЉЪБЃЌЪдВТЯыsinЁЯCABЕФжЕЃЎЃЈгУКЌaЕФДњЪ§ЪНБэЪОЃЌжБНгаДГіНсЙћЃЉ
ЁОД№АИЁПЃЈ1ЃЉAE=CEЃЛЃЈ2ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉСЌНгAEЁЂDEЃЌШчЭМ1ЃЌИљОндВжмНЧЖЈРэПЩЕУЁЯADE=ЁЯABE=90ЁуЃЌгЩгкAD=DCЃЌИљОнДЙжБЦНЗжЯпЕФаджЪПЩЕУAE=CEЃЛ
ЃЈ2ЃЉСЌНгAEЁЂEDЃЌШчЭМ2ЃЌгЩЁЯABE=90ЁуПЩЕУAEЪЧЁбOЕФжБОЖЃЌИљОнЧаЯпЕФаджЪПЩЕУЁЯAEF=90ЁуЃЌДгЖјПЩжЄЕНЁїADEЁзЁїAEFЃЌШЛКѓдЫгУЯрЫЦШ§НЧаЮЕФаджЪПЩЕУ![]() =ADAFЃЎЂйЕБCF=CDЪБЃЌПЩЕУ
=ADAFЃЎЂйЕБCF=CDЪБЃЌПЩЕУ![]() ЃЌДгЖјгаEC=AE=
ЃЌДгЖјгаEC=AE=![]() CDЃЌдкRtЁїDECжадЫгУШ§НЧКЏЪ§ПЩЕУsinЁЯCED=
CDЃЌдкRtЁїDECжадЫгУШ§НЧКЏЪ§ПЩЕУsinЁЯCED=![]() ЃЌИљОндВжмНЧЖЈРэПЩЕУЁЯCAB=ЁЯDECЃЌМДПЩЧѓГіsinЁЯCABЕФжЕЃЛЂкЕБCF=aCDЃЈaЃО0ЃЉЪБЃЌЭЌЂйМДПЩНтОіЮЪЬтЃЎ
ЃЌИљОндВжмНЧЖЈРэПЩЕУЁЯCAB=ЁЯDECЃЌМДПЩЧѓГіsinЁЯCABЕФжЕЃЛЂкЕБCF=aCDЃЈaЃО0ЃЉЪБЃЌЭЌЂйМДПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉAE=CEЃЎРэгЩЃК
СЌНгAEЁЂDEЃЌШчЭМ1ЃЌЁпЁЯABC=90ЁуЃЌЁрЁЯABE=90ЃЌЁрЁЯADE=ЁЯABE=90ЁуЃЌЁпAD=DCЃЌЁрAE=CEЃЛ
ЃЈ2ЃЉСЌНгAEЁЂEDЃЌШчЭМ2ЃЌЁпЁЯABE=90ЁуЃЌЁрAEЪЧЁбOЕФжБОЖЃЌЁпEFЪЧЁбOOЕФЧаЯпЃЌЁрЁЯAEF=90ЁуЃЌЁрЁЯADE=ЁЯAEF=90ЁуЃЌгжЁпЁЯDAE=ЁЯEAFЃЌЁрЁїADEЁзЁїAEFЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() =ADAFЃЎ
=ADAFЃЎ
ЂйЕБCF=CDЪБЃЌAD=DC=CFЃЌAF=3DCЃЌЁр![]() =DC3DC=
=DC3DC=![]() ЃЌЁрAE=
ЃЌЁрAE=![]() DCЃЌЁпEC=AEЃЌЁрEC=
DCЃЌЁпEC=AEЃЌЁрEC=![]() DCЃЌЁрsinЁЯCAB=sinЁЯCED=
DCЃЌЁрsinЁЯCAB=sinЁЯCED=![]() =
=![]() =
=![]() ЃЛ
ЃЛ
ЂкЕБCF=aCDЃЈaЃО0ЃЉЪБЃЌsinЁЯCAB=![]() ЃЎ
ЃЎ
ЁпCF=aCDЃЌAD=DCЃЌЁрAF=AD+DC+CF=ЃЈa+2ЃЉCDЃЌЁр![]() =DCЃЈa+2ЃЉDC=ЃЈa+2ЃЉ
=DCЃЈa+2ЃЉDC=ЃЈa+2ЃЉ![]() ЃЌЁрAE=
ЃЌЁрAE=![]() DCЃЌЁпEC=AEЃЌЁрEC=
DCЃЌЁпEC=AEЃЌЁрEC=![]() DCЃЌЁрsinЁЯCAB=sinЁЯCED=
DCЃЌЁрsinЁЯCAB=sinЁЯCED=![]() =
=![]() ЃЎ
ЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(10Зж)ФГЕчФдОЯњЩЬМЦЛЎЭЌЪБЙКНјвЛХњЕчФдЛњЯфКЭвКОЇЯдЪОЦїЃЌШєЙКНјЕчФдЛњЯф10 ЬЈКЭ
вКОЇЯдЪОЦї8ЬЈЃЌЙВашвЊзЪН№7000 дЊЃЛШєЙКНјЕчФдЛњЯф2ЬЈКЭвКОЇЯдЪОЦї5ЬЈ,ЙВашвЊзЪН№
4120дЊ.
(1)УПКЯЕчФдЛњЯфЁЂвКОЇЯдЪОЦїЕФНјМлИїЪЧЖрЩйдЊЃП
(2)ИУОЯњЩЬМЦЛЎЙКНјетСНжжЩЬЦЗЙВ50ЬЈЃЌЖјПЩгУгкЙКТђетСНжжЩЬЦЗЕФзЪН№ВЛГЌЙ§22240дЊ. ИљОнЪаГЁааЧщЃЌЯњЪлЕчФдЛњЯфЁЂвКОЇЯдЪОЦївЛЬЈЗжБ№ПЩЛёРћ10дЊКЭ160дЊ. ИУОЯњЩЬЯЃЭћЯњЪлЭъетСНжжЩЬЦЗЃЌЫљЛёРћШѓВЛЩйгк4100дЊ. ЪдЮЪЃКИУОЯњЩЬгаФФМИжжНјЛѕЗНАИЃПФФжжЗНАИЛёРћзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋХзЮяЯпy=Љ5x2+1ЯШЯђзѓЦНвЦ3ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ2ИіЕЅЮЛЃЌЫљЕУХзЮяЯпЕФНтЮіЪНЮЊЃЈ ЃЉ
A.y=Љ5ЃЈx+3ЃЉ2Љ2
B.y=Љ5ЃЈx+3ЃЉ2Љ1
C.y=Љ5ЃЈxЉ3ЃЉ2Љ2
D.y=Љ5ЃЈxЉ3ЃЉ2Љ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФБпаЮABCDЃЌНіДгЯТСаЬѕМўжаШЮШЁСНИіМгвдзщКЯЃЌЪЙЕУABCDЪЧЦНааЫФБпаЮЃЌвЛЙВгаЖрЩйжжВЛЭЌЕФзщКЯЃП ABЁЮCD BCЁЮAD AB=CD BC=ADЃЈ ЃЉ
A.2зщ
B.3зщ
C.4зщ
D.6зщ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНааЫФБпаЮЕФвЛзщЖдНЧЖШЪ§жЎКЭЮЊ200ЁуЃЌдђЦНааЫФБпаЮжаНЯДѓЕФНЧЮЊ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгУЭЌбљЙцИёЕФКкАзСНЩЋе§ЗНаЮДЩзЉЦЬЩшОиаЮЕиУцЃЌЧыЙлВьЯТСаЭМаЮЃЌЬНОПВЂЙлВьЯТСаЮЪЬтЁЃ

ЃЈ1ЃЉдкЕк4ИіЭМжаЃЌЙВгаАзЩЋДЩзЉ ПщЃЛдкЕк![]() ИіЭМжаЃЌЙВгаАзЩЋДЩзЉ ПщЃЛ
ИіЭМжаЃЌЙВгаАзЩЋДЩзЉ ПщЃЛ
ЃЈ2ЃЉдкЕк4ИіЭМжаЃЌЙВгаДЩзЉ ПщЃЛдкЕк![]() ИіЭМжаЃЌЙВгаДЩзЉ ПщЃЛ
ИіЭМжаЃЌЙВгаДЩзЉ ПщЃЛ
ЃЈ3ЃЉШчЙћУППщКкДЩзЉ4дЊЃЌАзДЩзЉ3дЊЃЌЦЬЩшЕБ![]() ЪБЃЌЙВашЛЈЖрЩйЧЎЙКТђДЩзЉЃП
ЪБЃЌЙВашЛЈЖрЩйЧЎЙКТђДЩзЉЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФБпаЮABCDжа,AD=BC,ШєЫФБпаЮABCDЪЧЦНааЫФБпаЮ,дђЛЙгІТњзу( )
A.ЁЯA+ЁЯC=180Ёу
B.ЁЯB+ЁЯD=180Ёу
C.ЁЯA+ЁЯB=180Ёу
D.ЁЯA+ЁЯD=180Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЕуЃЈmЉ1ЃЌЉ1ЃЉгыЕуЃЈ5ЃЌЉ1ЃЉЙигкyжсЖдГЦЃЌдђmЃНЃЈЁЁЁЁЃЉ
A.4B.Љ4C.5D.Љ5
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com