【题目】解方程组：
（1）
(2) 
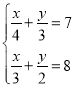
【答案】（1）
；（2）
【解析】
（1）
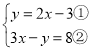，由①得2x-y=3③，②-③可求得x，将x值代入①可得y值，即可求得方程组的解．
（2）
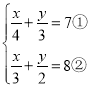，先将①×12去分母，将分式方程化为整式方程，得3x+4y=84③，将②×6，由分式方程化为整式方程，得2x+3y=48④，③和④再利用加减消元法即可求解方程组的解．
（1）
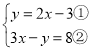
由①，得2x-y=3③
②-③，得x=5
将x=5代入①，得2×5-y=3
∴y=7
故方程组的解为：
故答案为：
（2）
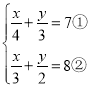
①×12，得3x+4y=84③
②×6，得2x+3y=48④
③×2，得6x+8y=168⑤
④×3，得6x+9y=144⑥
⑤-⑥，得y=-24
将y=-24代入①，得
∴x=60
故方程组的解为：
故答案为：
科目：初中数学 来源： 题型：
【题目】设M（m，n）在反比例函数y=﹣ 
上，其中m是分式方程 
﹣1= 
的根，将M点先向上平移4个单位，再向左平移1个单位，得到点N．若点M，N都在直线y=kx+b上，直线解析式为（ ）
A.y=﹣ 
x﹣ 
B.y= x+
C.y=4x﹣5
D.y=﹣4x+5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】利用我们学过的知识，可以导出下面这个形式优美的等式：a2+b2+c2﹣ab﹣bc﹣ac=
[(a﹣b)2+(b﹣c)2+(a﹣c)2]，该等式从左到右的变形，不仅保持了结构的对称性，还体现了数学的和谐、简洁、美观．
（1）请你检验说明这个等式的正确性．
（2）若a=2019，b=2020，c=2021，你能很快求出a2+b2+c2﹣ab﹣bc﹣ac的值吗？
（3）若a﹣b=
，b﹣c=，且a2+b2+c2=1，求ab+bc+ac的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF＝45°，将△DAE绕点D按逆时针方向旋转90°得到△DCM．
（1）求证：EF＝MF；（2）当AE＝1时，求EF的长．
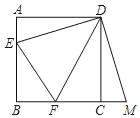
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】你能比较
与
的大小吗?为了解决这个问题，先把问题一般化.即比较
与
的大小(整数n≥1)．然后，从分析n=1，n=2， n=3，……这些简单情形入手，从中发现规律，经过归纳、猜想，得出结论.
（1）通过计算，比较下列①到⑥各组中两个数的大小：
① 
② 
③
④
⑤
⑥
（2）从（1）小题的结果归纳，请猜想与的大小关系：
（3）根据上面归纳猜想到的一般结论，可以得到：
_______ (填“>”、“=”或“<”)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1是一个长为4a、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）
（1）观察图2请你写出（a+b）2、（a﹣b）2、ab之间的等量关系是 ；
（2）根据（1）中的结论，若x+y＝5，xy＝
，则x﹣y＝ ；
（3）拓展应用：若（2019﹣m）2+（m﹣2020）2＝15，求（2019﹣m）（m﹣2020）的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（问题背景）
（1）如图1的图形我们把它称为“8字形”，请说理证明∠A+∠B＝∠C+∠D
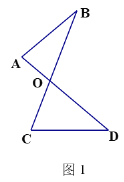
（简单应用）
（2）如图2，AP、CP分别平分∠BAD、∠BCD，若∠ABC＝28°，∠ADC＝20°，求∠P的度数（可直接使用问题（1）中的结论）
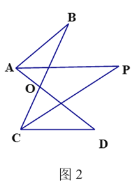
（问题探究）
（3）如图3，直线BP平分∠ABC的外角∠FBC，DP平分∠ADC的外角∠ADE，若∠A＝30°，∠C＝18°，则∠P的度数为
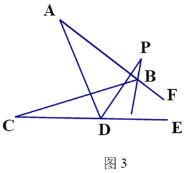
（拓展延伸）
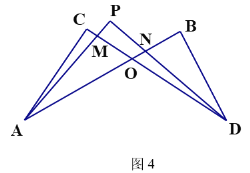
（4）在图4中，若设∠C＝x，∠B＝y，∠CAP＝
∠CAB，∠CDP＝∠CDB，试问∠P与∠C、∠B之间的数量关系为 （用x、y表示∠P）
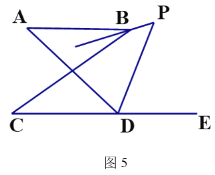
（5）在图5中，BP平分∠ABC，DP平分∠ADC的外角∠ADE，猜想∠P与∠A、∠C的关系，直接写出结论 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AH是⊙O的直径，AE平分∠FAH，交⊙O于点E，过点E的直线FG⊥AF，垂足为F，B为半径OH上一点，点E，F分别在矩形ABCD的边BC和CD上．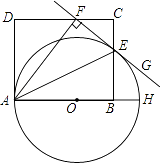
（1）求证：直线FG是⊙O的切线；
（2）若CD=10，EB=5，求⊙O的直径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正三角形ABC中，D，E，F分别是BC，AC，AB上的点，DE⊥AC，EF⊥AB，FD⊥BC，则△DEF的面积与△ABC的面积之比等于 ．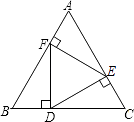 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com