

分析 (1)此题根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积,一种是大正方形的面积,可得等式(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
(2)利用S阴影=正方形ABCD的面积+正方形ECGF的面积-三角形BGF的面积-三角形ABD的面积求解.
解答 解:(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac
(2)∵a+b=10,ab=20,
∴S阴影=a2+b2-$\frac{1}{2}$(a+b)•b-$\frac{1}{2}$a2=$\frac{1}{2}$a2+$\frac{1}{2}$b2-$\frac{1}{2}$ab=$\frac{1}{2}$(a+b)2-$\frac{3}{2}$ab=$\frac{1}{2}$×102-$\frac{3}{2}$×20=50-30=20.
点评 本题考查了完全平方公式几何意义,解题的关键是注意图形的分割与拼合,会用不同的方法表示同一图形的面积.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:选择题
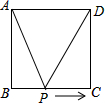 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm)在下列图象中,表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm)在下列图象中,表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )| A. |  | B. |  | C. |  | D. | 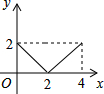 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
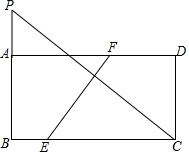 已知:如图,将矩形ABCD沿EF折叠,折痕交BC于点E,交AD于点F.若折叠后点C落在BA的延长线上P处,且AP=2,AB=4,AD=8,求折痕EF的长.
已知:如图,将矩形ABCD沿EF折叠,折痕交BC于点E,交AD于点F.若折叠后点C落在BA的延长线上P处,且AP=2,AB=4,AD=8,求折痕EF的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com