
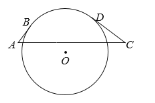
【题目】如图,AB、CD是⊙O的切线,B、D为切点,AB=2,CD=4,AC=10.若∠A+∠C=90°,则⊙O的半径是_______.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,-2),连接BC、AD.
轴交于点C,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,-2),连接BC、AD.
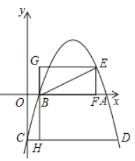
(1)将矩形OBHC绕点B按逆时针旋转90°后,再沿![]() 轴对折到矩形GBFE(点C与点E对应,点O与点G对应),求点E的坐标;
轴对折到矩形GBFE(点C与点E对应,点O与点G对应),求点E的坐标;
(2)设过点E的直线交AB于点P,交CD于点Q.
①当四边形PQCB为平行四边形时,求点P的坐标;
②是否存在点P,使直线PQ分梯形ADCB的面积为1∶3两部分?若存在,求出点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
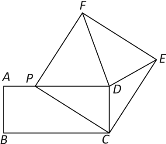
【题目】如图,已知在矩形ABCD中,AD=10cm,AB=4cm,动点P从点A出发,以2cm/s的速度沿AD向终点D移动,设移动时间为![]() (s) .连接PC,以PC为一边作正方形PCEF,连接DE、DF.
(s) .连接PC,以PC为一边作正方形PCEF,连接DE、DF.
(1)求正方形PCEF的面积(用含![]() 的代数式来表示,不要求化简),并求当正方形PCEF的面积为25 cm2时
的代数式来表示,不要求化简),并求当正方形PCEF的面积为25 cm2时![]() 的值;
的值;
(2)设△DEF的面积为![]() (cm2),求
(cm2),求![]() 与
与![]() 之间的函数关系式,并求当
之间的函数关系式,并求当![]() 为何值时?△DEF的面积取得最小值,这个最小值是多少?
为何值时?△DEF的面积取得最小值,这个最小值是多少?
(3)求当![]() 为何值时?△DEF为等腰三角形.
为何值时?△DEF为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
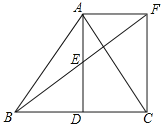
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
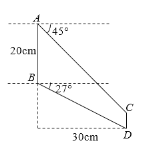
【题目】某校航模小组打算制作模型飞机,设计了如图所示的模型飞机机翼图纸.图纸中AB∥CD,均与水平方向垂直,机翼前缘AC、机翼后缘BD与水平方向形成的夹角度数分别为45°、27°,AB=20cm,点D到直线AB的距离为30cm.求机翼外缘CD的长度.(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
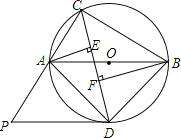
(1)求证:EF +AE= BF ;
(2)求证:△PDA∽△PCD ;
(3)若AC=6,BC=8,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
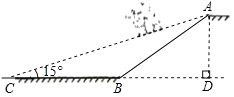
【题目】若商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,扶梯AB的坡度i为1:![]() .改造后的斜坡式动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度.
.改造后的斜坡式动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度.
(结果精确到0.1m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字0,1,2,3的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽出一张卡片,则抽到数字“2”的概率为 ;
(2)随机抽出一张卡片,记下数字后放回并搅匀,再随机抽出一张卡片,请用列表或画树状图的方法,求两次抽出的卡片上的数字之和是3的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com