
 如图,抛物线y=x2+bx+c经过直线y=x-4与坐标轴的两个交点A、B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
如图,抛物线y=x2+bx+c经过直线y=x-4与坐标轴的两个交点A、B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.分析 (1)令直线y=x-4的x、y分别为0可求得点B和A的坐标,将点A、B的坐标代入抛物线的解析式可求得b、c的值,最后依据配方法可求得顶点D的坐标;
(2)记AB与对称轴的交点为M,利用抛物线的对称性可求得点C的坐标,由轴对称的性质可知AM=CM,故此可知BM+CM=BM+MA,当点A、B、M在同一条直线上时MB+CM由最小值,然后依据两点间的距离公式分别求得BC与AB的长,从而可求得△MBC周长的最小值;
(3)如图2所示,当点P在y轴左侧时,过点P作PE⊥x,交直线AB与点M.设点P的坐标为(x,x2-3x-4),则点F的坐标为(x,x-4),可求得PF=x2-4x.接下来由S△PAB=S△PAF-S△PFB,求得S与x的函数关系式,然后依据x的范围以及函数的增减性可确定出S的范围以及符合条件的点P的个数;如图3所示:当点P在y轴的右侧时.设点P的坐标为(x,x2-3x-4),则点F的坐标为(x,x-4),PF=-x2+4x,由S△PAB=S△PAF+S△PFB可求得S与x的函数关系式,然后依据x的范围以及函数的增减性可确定出S的范围以及符合条件的点P的个数.
解答 解:(1)∵将y=0代入y=x-4得:x-4=0,解得:x=4,
∴点A的坐标为(4,0).
∵将x=0代入y=x-4得:y=-4,
∴点B的坐标为(0,-4).
∵将点A、点B的坐标代入抛物线的解析式得:$\left\{\begin{array}{l}{c=-4}\\{16+4b+c=0}\end{array}\right.$,解得:c=-4,b=-3.
∴抛物线的解析式为y=x2-3x-4.
∴y=(x-$\frac{3}{2}$)2-$\frac{25}{4}$.
∴点D的坐标为($\frac{3}{2}$,-$\frac{25}{4}$).
(2)如图1所示:记AB与对称轴的交点为M.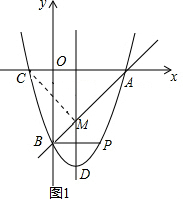
∵点A与点C关于直线x=$\frac{3}{2}$,
∴CM=AM,点C的坐标为(-1,0).
∴MC+MB=AM+AC=AB.
∵BC的长度不变,
∴当MC+MB最短时,三角形的周长最小.
∴当点A、B、M在一条直线上时,△BCM的周长有最小值.
由两点间的距离公式可知BC=$\sqrt{(-1-0)^{2}+(-4-0)^{2}}$=$\sqrt{17}$,AB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
∴△BCM的周长=BC+CM+MB=CB+CM+MA=CB+AB=$\sqrt{17}$+4$\sqrt{2}$.
(3)①如图2所示:当点P在y轴左侧时,过点P作PE⊥x,交直线AB与点M.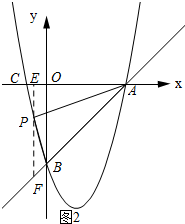
设点P的坐标为(x,x2-3x-4),则点F的坐标为(x,x-4),PF=x2-3x-4-(x-4)=x2-4x.
∵S△PAB=S△PAF-S△PFB=$\frac{1}{2}PF•OA$=2x2-8x.
∴S=2x2-8x(-1<x<0).
∵x=-$\frac{b}{2a}$=$\frac{8}{2×2}$=2,
∴当-1<x<0时,S随x的增大而减小.
当x=-1时,S=10,当x=0时,S=0,
∴0<S<10,此时符合条件的点P有9个.
②如图3所示:当点P在y轴的右侧时.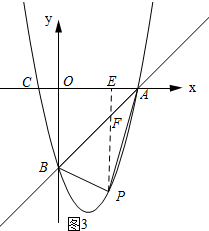
设点P的坐标为(x,x2-3x-4),则点F的坐标为(x,x-4),PF=x-4-(x2-3x-4)=-x2+4x.
∵S△PAB=S△PAF+S△PFB=$\frac{1}{2}PF•OA$=-2x2+8x.
∴S=-2x2+8x(0<x<4).
∵x=-$\frac{b}{2a}$=-$\frac{8}{-2×2}$=2,
∴当x=2时,S有最大值,S的最大值=8,当x=0或x=4时,S=0.
∴0<S<8,符合条件的点P有14个.
综上所述:S的取值范围是0<S<10,S为整数时,△PAB的共有23个.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、轴对称图形的性质、两点间的距离公式、二次函数的图象和性质,求得S与点P的横坐标x之间的函数关系式是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系xOy,点B的坐标为(2,0),若抛物线y=$\frac{1}{2}$x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-2<k<$\frac{1}{2}$.
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系xOy,点B的坐标为(2,0),若抛物线y=$\frac{1}{2}$x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-2<k<$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:判断题
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
⑴请画出平移后的△A′B′C′.
(2)△A′B′C′的面积为_________.
(3)若连接AA′,CC′,则这两条线段之间的关系是_______________.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,直线 、
、 与直线
与直线 相交,给出下列条件:
相交,给出下列条件:
①∠1=∠2; ②∠3=∠6; ③∠4+∠7=180°; ④∠5+∠3=180°,
其中能判断 ∥
∥ 的是( )
的是( )

A. ①②③④ B. ①③④ C. ①③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )
如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
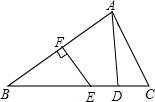 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC.
如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com