
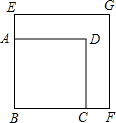
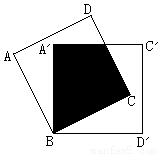
 如图,将两个正方形纸片ABCD和EBFG重叠,且使直角B完全重合,然后用剪刀将它剪成若干小纸片,恰能拼成一个大正方形.请用两次剪断(按直线剪断算一次)完成此项任务,用虚线在图上画出剪痕.
如图,将两个正方形纸片ABCD和EBFG重叠,且使直角B完全重合,然后用剪刀将它剪成若干小纸片,恰能拼成一个大正方形.请用两次剪断(按直线剪断算一次)完成此项任务,用虚线在图上画出剪痕.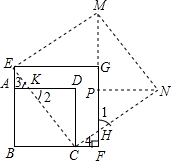 解:如图,连接HN,EC与AD交于点K,作CH⊥EC交GF于点H,则EC、CH即为剪痕;
解:如图,连接HN,EC与AD交于点K,作CH⊥EC交GF于点H,则EC、CH即为剪痕;
|


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
 如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为4
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年九年级期末数学试卷 题型:填空题
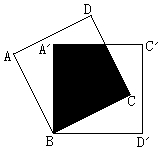
如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为cm2,则这个旋转角度为________度。(考查正方形、三角形等)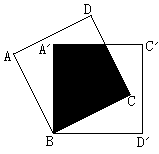
查看答案和解析>>
科目:初中数学 来源:2012届九年级期末数学试卷 题型:填空题
如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为cm2,则这个旋转角度为________度。(考查正方形、三角形等)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com