已知抛物线y=x2+bx-c与x轴两交点的坐标分别为A(m,0),B(-3m,0)(m<0).
(1)证明:b2+4c>0;
(2)证明:4c=3b2;
(3)若该函数图象与y轴相交于点C,且△ABC的面积为6,求这个二次函数的最小值.
【答案】
分析:(1)根据已知,方程x
2+bx-c=0有两个不同的实根,所以△=b
2-4ac>0代入求出即可;
(2)根据已知得出m,-3m是一元二次方程x
2+bx-c=0的两根,再利用根与系数的关系得出b,c与m的关系即可;
(3)首先得出AB=-3m-m=-4m=-2b,OC=|-c|=c,再利用三角形面积公式得出关于b的方程求出即可.
解答:(1)证明:由已知,方程x
2+bx-c=0有两个不同的实根,
所以△=b
2-4×1×(-c)=b
2+4c>0;
(2)证明:依题意,m,-3m是一元二次方程x
2+bx-c=0的两根.
根据一元二次方程根与系数的关系,得m+(-3m)=-b,m×(-3m)=-c.
则b=2m<0,c=3m
2>0.
则4c=3b
2=12m
2.
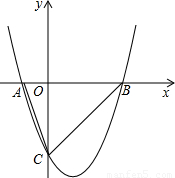
(3)解:依题意,AB=-3m-m=-4m=-2b,OC=|-c|=c,
因为△ABC的面积=
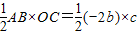
=6,
由(2)知,4c=3b
2,所以
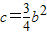
,
由
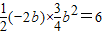
,
解得 b=-2,
则c=

b
2=

×(-2)
2=3.
则y=x
2-2x-3=(x-1)
2-4.
故二次函数的最小值为-4.
点评:此题主要考查了一元二次方程中根与系数的关系以及根的判别式和三角形面积求法、二次函数最值求法等知识,利用根与系数关系得出b,c之间的关系是解题关键.


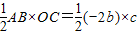 =6,
=6,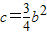 ,
,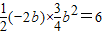 ,
, b2=
b2= ×(-2)2=3.
×(-2)2=3.

 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.