
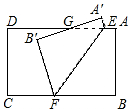
 如图,把长方形纸片ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=50°,则∠AEF=115°.
如图,把长方形纸片ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=50°,则∠AEF=115°. 分析 根据AE∥BF,可得∠AEF+∠BFE=180°,再根据折叠变换的性质得:∠BFE=∠B'FE,而∠CFB′=50°,进而得到∠BFE=(180°-50°)÷2=65°,最后得出∠AEF=180°-65°=115°.
解答  解:如图,∵四边形ABCD为长方形,
解:如图,∵四边形ABCD为长方形,
∴AE∥BF,
∴∠AEF+∠BFE=180°,
由折叠变换的性质得:
∠BFE=∠B'FE,而∠CFB′=50°,
∴∠BFE=(180°-50°)÷2=65°,
∴∠AEF=180°-65°=115°.
故答案为:115°.
点评 本题主要考查了翻折变换的性质、矩形的性质、平行线的性质,解决问题的关键是掌握矩形的性质、平行线的性质等几何知识点.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
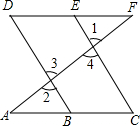 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9800名学生是总体 | |
| B. | 每个学生是个体 | |
| C. | 100名学生是所抽取的一个样本 | |
| D. | 100名学生的视力情况是所抽取的一个样本 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com