
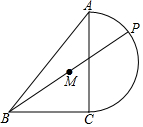
 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )| A. | 2$\sqrt{2}$π | B. | $\sqrt{2}$π | C. | 2π | D. | 2$\sqrt{2}$ |
分析 如图,连接PA、PC,取AB、BC的中点E、F,连接EF、EM、FM.首先证明∠EMF=90°,推出点M的轨迹是$\widehat{EF}$,即EF为直径的半圆,图中红线部分,由此即可解决问题.
解答 解:如图,连接PA、PC,取AB、BC的中点E、F,连接EF、EM、FM.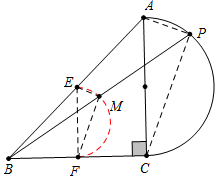
∵AC是直径,
∴∠APC=90°,
∵BE=EA,BM=MP,
∴EM∥PA,同理FM∥PC,
∴∠BME=∠BPA,∠BMF=∠BPC,
∴∠BME+∠BMF=∠BPA+∠BPC=90°,
∴∠EMF=90°,
∴点M的轨迹是$\widehat{EF}$,(EF为直径的半圆,图中红线部分)
∵BC=AC,∠ACB=90°,AB=8,
∴AC=4$\sqrt{2}$,EF=$\frac{1}{2}$AC=2$\sqrt{2}$,
∴$\widehat{EF}$的长=π•$\sqrt{2}$=$\sqrt{2}$π.
故选B.
点评 本题考查轨迹、等腰直角三角形的性质、圆的有关知识、弧长公式等知识,解题的关键是正确寻找点M的运动轨迹,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x-2}+1=0$ | B. | $\frac{x}{{{x^2}-1}}=\frac{1}{{{x^2}-1}}$ | C. | x5+32=0 | D. | 2x2+x+1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
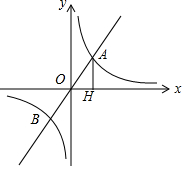 已知:如图,正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象相交于点A、B,点A在第一象限,且点A的横坐标为1,作AH垂直于x轴,垂足为点H,S△AOH=1.
已知:如图,正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象相交于点A、B,点A在第一象限,且点A的横坐标为1,作AH垂直于x轴,垂足为点H,S△AOH=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com