
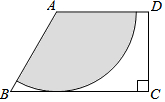
 如图,梯形ABCD中,AD∥BC,∠C=90°,∠B=60°,AB=4,以点A为圆心在这个梯形内画出一个最大的扇形(图中阴影部分),则这个扇形的面积是4π.
如图,梯形ABCD中,AD∥BC,∠C=90°,∠B=60°,AB=4,以点A为圆心在这个梯形内画出一个最大的扇形(图中阴影部分),则这个扇形的面积是4π. 科目:初中数学 来源: 题型:填空题
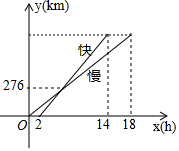 如图是一辆慢车与一辆快车沿相同路线从A地到B地所行的路程与时间之间的函数图象,已知慢车比快车早出发2小时,则A、B两地的距离为828 km.
如图是一辆慢车与一辆快车沿相同路线从A地到B地所行的路程与时间之间的函数图象,已知慢车比快车早出发2小时,则A、B两地的距离为828 km.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
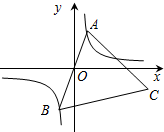 如图,已知:点A是双曲线y=$\frac{3}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$ (x>0)上运动,则k的值是-9.
如图,已知:点A是双曲线y=$\frac{3}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$ (x>0)上运动,则k的值是-9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠BAC=96°,延长BC到点D,∠ABC与∠ACD的平分线相交于点A1,则∠A1的大小是48°,∠A1BC和∠A1CD的平分线相交于点A2,依此类推,∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013的大小是$\frac{96°}{{2}^{2013}}$.
如图,△ABC中,∠BAC=96°,延长BC到点D,∠ABC与∠ACD的平分线相交于点A1,则∠A1的大小是48°,∠A1BC和∠A1CD的平分线相交于点A2,依此类推,∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013的大小是$\frac{96°}{{2}^{2013}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
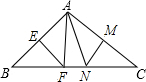 如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°.
如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com