
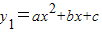 和一次函数y2=mx+n的图象,观察图象,写出y2≤y1时x的取值范围 .
和一次函数y2=mx+n的图象,观察图象,写出y2≤y1时x的取值范围 .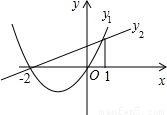
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
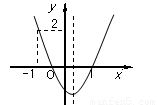
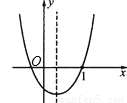
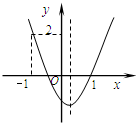 (2014•宁波一模)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②a+c=1;③2a+b<0;④b2-4ac>0.其中结论正确的个数为( )
(2014•宁波一模)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②a+c=1;③2a+b<0;④b2-4ac>0.其中结论正确的个数为( )查看答案和解析>>
科目:初中数学 来源:2012届浙江省富阳市永兴中学九年级上学期第二次知识检测数学试卷(带解析) 题型:填空题
如图,二次函数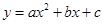 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与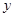 轴相交于负半轴.(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答,则只以第(2)问计分)
轴相交于负半轴.(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答,则只以第(2)问计分)
第(1)问:给出四个结论:①  ;②
;② 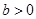 ;③
;③ 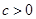 ;④
;④ 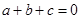 .
.
其中正确结论的序号是 .
第(2)问:给出四个结论:① 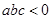 ;②
;② 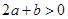 ;③
;③ 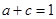 ;④
;④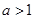 .其中正确结论的序号是 .
.其中正确结论的序号是 .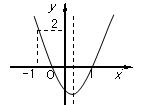
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省富阳市九年级上学期第二次知识检测数学试卷(解析版) 题型:填空题
如图,二次函数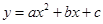 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与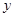 轴相交于负半轴.(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答,则只以第(2)问计分)
轴相交于负半轴.(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答,则只以第(2)问计分)
第(1)问:给出四个结论:① 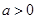 ;②
;② 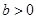 ;③
;③
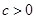 ;④
;④
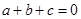 .
.
其中正确结论的序号是 .
第(2)问:给出四个结论:①  ;②
;② 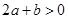 ;③
;③
 ;④
;④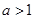 .其中正确结论的序号是
.
.其中正确结论的序号是
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
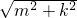 称为朋友距离.
称为朋友距离. 都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”.
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”. .
.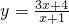 和它的基本函数
和它的基本函数 ,找到朋友路径,并求相应的朋友距离.
,找到朋友路径,并求相应的朋友距离.查看答案和解析>>
科目:初中数学 来源:2010年山东省东营市中考模拟考试五校联考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com