
����Ŀ����ͼ��CΪ��AOB�ı�OA��һ�㣬OC=6��NΪ��OB�����ڵ�O��һ���㣬P���߶�CN��һ�㣬����P�ֱ���PQ��OA��OB�ڵ�Q��PM��OB��OA�ڵ�M��
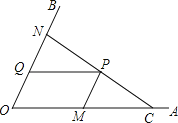
��1������AOB=45�㣬OM=4��OQ=![]() ����֤��CN��OB��
����֤��CN��OB��
��2������N�ڱ�OB���˶�ʱ���ı���OMPQʼ�ձ���Ϊ���Σ�
���ʣ�![]() ��ֵ�Ƿ����仯������仯�������ȡֵ��Χ��������䣬��˵�����ɣ�
��ֵ�Ƿ����仯������仯�������ȡֵ��Χ��������䣬��˵�����ɣ�
��������OMPQ�����ΪS1����NOC�����ΪS2����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1������������2���ٲ���仯������������0��![]() ��
��![]()
��������
��1����P��PE��OA��E��NF��OA�����ж��ı���OMPQΪƽ���ı��Σ�����������Ǻ��������PCE=45�������ɣ�
��2�������ı���OQPM�����Σ���OM=x��ON=y������OQ=QP=OM=x��NQ=y-x�������������ε��ж���֤��NQP�ס�NOC����![]() ���̶����ɵ�
���̶����ɵ�![]() ��ֵ�������仯��
��ֵ�������仯��
�ڹ�P��PE��OA����N��NF��OA�����жϳ���CPM�ס�CNO�ٵõ�����ʽ![]() ����⼴�ɣ�
����⼴�ɣ�
�⣺��1����ͼ1��
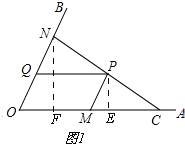
��P��PE��OA��E��NF��OA��
��PQ��OA��PM��OB��
���ı���OMPQΪƽ���ı��Σ�
��PM=OQ= ![]() ����PME=��AOB=45����
����PME=��AOB=45����
��PE=PMsin45��=1��ME=1��
��CE=OC��OM��ME=1��
��tan��PCE= ![]() =1��
=1��
���PCE=45����
���CNO=90����
��CN��OB��
��2����![]() ��ֵ�������仯��
��ֵ�������仯��
���ɣ���OM=x��ON=y��
���ı���OMPQΪ���Σ�
��OQ=QP=OM=x��NQ=y-x��
��PQ��OA��
���NQP=��O��
�ߡ�QNP=��ONC��
���NQP�ס�NOC��
�� ![]() ��
��
�� ![]() ��
��
��6y��6x=xy��
��![]() ��
��
��![]() ��
��
����ͼ2��
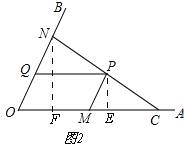
��P��PE��OA����N��NF��OA��
��S1=OM��PE��S2= ![]() OC��NF��
OC��NF��
��![]() ��
��
��PM��OB��
���PMC=��NOC��
�ߡ�PCM=��NCO��
���CPM�ס�CNO��
�� ![]() ��
��
�� ![]() ��
��
��0��x��6��
��0��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijѧУ���AB�Ա���һ������ʱ��ģ�ͣ�ʱ�ӵ�9���3��Ŀ̶��߸պú͵����غϣ���Բ�İ뾶2m����˵ĵ�A������9��̶�C�ľ���Ϊ11m��һ��С���۲쵽��������˶���B��Ӱ�Ӹպ�Ͷ��ʱ�ӵ�11��Ŀ̶��ϣ�ͬʱ���1�׳��ı�˵�Ӱ��1.2m�������AB�ĸ߶ȣ�
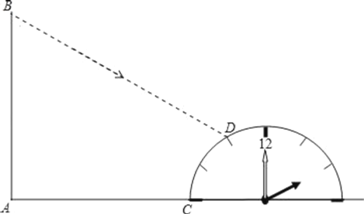
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ��߶�
�õ��߶�![]() ��˫����
��˫����![]() ������
������![]() .
.

��1����ֱ��![]() ��˫����
��˫����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��ƽ��ֱ��![]() ��ʹ����˫����
��ʹ����˫����![]() ��Ψһ������
��Ψһ������![]() ʱ�����
ʱ�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() �У�
��![]() ��
��![]() ���
���![]() ��
��![]() ��
��![]() ���е㣬��
���е㣬��![]() ΪԲ�ģ��߶�
ΪԲ�ģ��߶�![]() �ij�Ϊ�뾶��Բ�Ľ�Ϊ
�ij�Ϊ�뾶��Բ�Ľ�Ϊ![]() ������
������![]() ����
����![]() ������
������![]() ����ͼ����Ӱ���ֵ����Ϊ_______ƽ����λ��
����ͼ����Ӱ���ֵ����Ϊ_______ƽ����λ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣���ͼ���ִ���B����ÿСʱ60������ٶ�����ƫ��20�㷽�����ٺ��У���B���۲����Aλ����ƫ��50�㷽���ϣ��ִ�����40���ӵ���C������C���۲����Aλ�ڱ�ƫ��10�㷽���ϣ���C�������A�ľ����ǣ� ��

A��20���� B��40���� C��![]() ���� D��
���� D��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
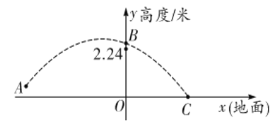
����Ŀ��2019��Ů�����籭��9�����ձ����У��й�Ů����ʮһ��ʤ�Ľ��˳ɼ�����ھ������չ�����Ŷ�Э������ǿƴ����Ů�ž�����ͼ��ij�α����е���ʱ�Ķ��������������������˶�·�߽��ƵĿ��������ߣ���ͬһ��ֱƽ���ڽ�����ͼ��ʾ��ֱ������ϵ����֪�˶�Ա����ʱ��ͼ�е�![]() ����������ˮƽ����Ϊ5�ף����������Ĵ�ֱ����Ϊ0.5�ף������������϶�0.26�״���ͼ�е�
����������ˮƽ����Ϊ5�ף����������Ĵ�ֱ����Ϊ0.5�ף������������϶�0.26�״���ͼ�е�![]() ��Խ��������Ů���������������϶˾����ĸ߶�Ϊ2.24�ף������ʱ��ͼ�е�
��Խ��������Ů���������������϶˾����ĸ߶�Ϊ2.24�ף������ʱ��ͼ�е�![]() ����������ˮƽ����Ϊ2.5�ף��������˶�·�ߵĺ�������ʽΪ�� ��
����������ˮƽ����Ϊ2.5�ף��������˶�·�ߵĺ�������ʽΪ�� ��

A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҩƷ�������ع���5�������ߣ�ÿ��������ÿ������ҩƷ20��У��û��ش���ӵ�һ���¿�ʼ��������½�������ÿ�������߽����������죮����ʱ��ÿ����ֻ��������һ�������ߣ����������ߵ���ͣ���������¸���Ͷ�����������������������������������飬ÿ�����������������ÿ�µIJ������ԭ�����20%��
��1���������⣬����������⣺
�ٰ��±�����������ֱ��д�ں����ϣ���
���� | ��1���� | ��2���� | ��3���� | ��4���� | ��5���� | ��6���� | �� |
����/��� | �� �� | �� �� | �� �� | 92 | �� | �� | �� |
�ڴӵ�1���½�������������� �����µIJ�����ʼ����δ��������ʱ�IJ�����
��2�����û��ص�x���£�1��x��5����x���������IJ���Ϊy��У���y����x�ĺ�����ϵʽ��
��3����֪ÿ�������ߵ������������30��Ԫ��ÿ��ҩƷ�ɻ���3Ԫ����ӵ�1���¿�ʼ�������������ҩƷ����������ΪW1��Ԫ��ͬʱ���ڣ���������������������ΪW2��Ԫ�����ٵ���n���£�nΪ��������ʱ��W1����W2����n��ֵ����������������ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����������Ա�����������ȡ������������չ����֪ʶ�н��ʴ������õõ������ݻ�������ͼ��ʾ����ͳ��ͼ���÷�Ϊ����������Ϊ10�֣���ͷ�Ϊ6�֣���
�����ͼ����Ϣ������������⣺
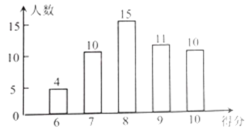
��1�����ε���һ����ȡ��__________������
��2���ε����ȡ���������ݵ�ƽ��������ֱ��д���������ݵ���������λ����
��3�����������Ը�С��500������չ�����н��ʴ�����10������Ϊ��һ�Ƚ��������ݵ����������������������Աֱ�ӹ��Ƴ��������ٷ���һ�Ƚ�����Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ӿ����ǻ�У�����裬ij����Ϊ�Ե�ѧУ�ɹ�һ�� ![]() ��
��![]() �����ͺŵ�һ����������г����鷢�֣�����ÿ��
�����ͺŵ�һ����������г����鷢�֣�����ÿ�� ![]() ��һ����ļ۸��ÿ��
��һ����ļ۸��ÿ�� ![]() ��һ����ļ۸��
��һ����ļ۸�� ![]() ��Ԫ������
��Ԫ������![]() ��Ԫǡ���ܹ���
��Ԫǡ���ܹ��� ![]() ��
�� ![]() ��һ�����
��һ����� ![]() ��
�� ![]() ��һ�����
��һ�����
��1�������ÿ�� ![]() �͡�
�͡�![]() ��һ����ļ۸���Ƕ�����Ԫ��
��һ����ļ۸���Ƕ�����Ԫ��
��2����������ƻ��ɹ� ![]() �͡�
�͡�![]() ��һ�����
��һ����� ![]() �ף���Ͷ���ʽ�
�ף���Ͷ���ʽ� ![]() ��Ԫ. ����������أ�Ԥ������ÿ��
��Ԫ. ����������أ�Ԥ������ÿ�� ![]() ��һ����ļ۸䣬ÿ��
��һ����ļ۸䣬ÿ�� ![]() ��һ����ļ۸�Ƚ�������
��һ����ļ۸�Ƚ������� ![]() �� ��������깺��
�� ��������깺�� ![]() ��һ���
��һ��� ![]() ��.
��.
����д������������Ͷ���ʽ� ![]() ����Ԫ���빺��
����Ԫ���빺�� ![]() ��һ���
��һ��� ![]() ���ף�֮��ĺ�����ϵʽ ��
���ף�֮��ĺ�����ϵʽ ��
�����������깺�� ![]() ��һ������ܷ��ò����ڹ���
��һ������ܷ��ò����ڹ��� ![]() ��һ������ܷ��ã���ô��������������ҪͶ�������Ԫ������ɲɹ��ƻ���
��һ������ܷ��ã���ô��������������ҪͶ�������Ԫ������ɲɹ��ƻ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com