试题分析:(1)把点A、B、C的坐标代入抛物线解析式,利用待定系数法求二次函数解析式解 答即可; (2)①根据点A、B的坐标求出OA=OB,从而得到△AOB是等腰直角三角形,根据等腰直角三角形的性质可得∠BAO=45°,然后求出△PED是等腰直角三角形,根据等腰直角三角形的性质,PD越大,△PDE的周长最大,再判断出当与直线AB平行的直线与抛物线只有一个交点时,PD最大,再求出直线AB的解析式为y=x+3,设与AB平行的直线解析式为y=x+m,与抛物线解析式联立消掉y,得到关于x的一元二次方程,利用根的判别式△=0列式求出m的值,再求出x、y的值,从而得到点P的坐标; ②先确定出抛物线的对称轴,然后(i)分点M在对称轴上时,过点P作PQ⊥对称轴于Q,根据同角的余角相等求出∠APF=∠QPM,再利用“角角边”证明△APF和△MPQ全等,根据全等三角形对应边相等可得PF=PQ,设点P的横坐标为n,表示出PQ的长,即PF,然后代入抛物线解析式计算即可得解;(ii)点N在对称轴上时,同理求出△APF和△ANQ全等,根据全等三角形对应边相等可得PF=AQ,根据点A的坐标求出点P的纵坐标,再代入抛物线解析式求出横坐标,即可得到点P的坐标.
试题解析:(1)∵抛物线y=ax
2+bx+c经过点A(﹣3,0),B(0,3),C(1,0),
∴

,
解得

,
所以,抛物线的解析式为y=﹣x
2﹣2x+3;
(2)①∵A(﹣3,0),B(0,3),
∴OA=OB=3,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
∵PF⊥x轴,
∴∠AEF=90°﹣45°=45°,
又∵PD⊥AB,
∴△PDE是等腰直角三角形,
∴PD越大,△PDE的周长越大,
易得直线AB的解析式为y=x+3,
设与AB平行的直线解析式为y=x+m,
联立

,
消掉y得,x
2+3x+m﹣3=0,
当△=3
2﹣4×1×(m﹣3)=0,
即m=

时,直线与抛物线只有一个交点,PD最长,
此时x=

,y=

+

=

,
∴点P(

,

)时,△PDE的周长最大;
②抛物线y=﹣x
2﹣2x+3的对称轴为直线x=

,
(i)如图1,点M在对称轴上时,过点P作PQ⊥对称轴于Q,

在正方形APMN中,AP=PM,∠APM=90°,
∴∠APF+∠FPM=90°,∠QPM+∠FPM=90°,
∴∠APF=∠QPM,
∵在△APF和△MPQ中,

,
∴△APF≌△MPQ(AAS),
∴PF=PQ,
设点P的横坐标为n(n<0),则PQ=﹣1﹣n,
即PF=﹣1﹣n,
∴点P的坐标为(n,﹣1﹣n),
∵点P在抛物线y=﹣x
2﹣2x+3上,
∴﹣n
2﹣2n+3=﹣1﹣n,
整理得,n
2+n﹣4=0,
解得n
1=

(舍去),n
2=

,
﹣1﹣n=﹣1﹣

=

,
所以,点P的坐标为(

,

);
(ii)如图2,点N在对称轴上时,设抛物线对称轴与x轴交于点Q,

∵∠PAF+∠FPA=90°,∠PAF+∠QAN=90°,
∴∠FPA=∠QAN,
又∵∠PFA=∠AQN=90°,PA=AN,
∴△APF≌△NAQ,
∴PF=AQ,
设点P坐标为P(x,﹣x
2﹣2x+3),
则有﹣x
2﹣2x+3=﹣1﹣(﹣3)=2,
解得x=

﹣1(不合题意,舍去)或x=﹣

﹣1,
此时点P坐标为(﹣

﹣1,2).
综上所述,当顶点M恰好落在抛物线对称轴上时,点P坐标为(

,

),当顶点N恰好落在抛物线对称轴上时,点P的坐标为(﹣

﹣1,2).

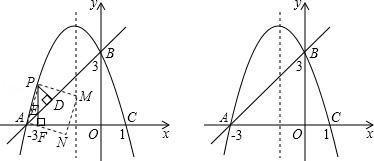
 ,
, )时,△PDE的周长最大;②当顶点M恰好落在抛物线对称轴上时,点P坐标为(
)时,△PDE的周长最大;②当顶点M恰好落在抛物线对称轴上时,点P坐标为( ,
, ),当顶点N恰好落在抛物线对称轴上时,点P的坐标为(﹣
),当顶点N恰好落在抛物线对称轴上时,点P的坐标为(﹣ ﹣1,2).
﹣1,2). ,
, ,
, ,
, 时,直线与抛物线只有一个交点,PD最长,
时,直线与抛物线只有一个交点,PD最长, ,y=
,y= +
+ =
= ,
, ,
, )时,△PDE的周长最大;
)时,△PDE的周长最大; ,
,
 ,
, (舍去),n2=
(舍去),n2= ,
, =
= ,
, ,
, );
);
 ﹣1(不合题意,舍去)或x=﹣
﹣1(不合题意,舍去)或x=﹣ ﹣1,
﹣1, ﹣1,2).
﹣1,2). ,
, ),当顶点N恰好落在抛物线对称轴上时,点P的坐标为(﹣
),当顶点N恰好落在抛物线对称轴上时,点P的坐标为(﹣ ﹣1,2).
﹣1,2).

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
 .
.

 (m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程
(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程 的两实数根是
的两实数根是