
通过阅读所得的启示回答问题.(阅读中的结论可直接用)

问题:某学校初三共有8个班进行辩论比赛,规定进行单循环赛(每两个班赛一场),那么,该初三年级的辩论赛共进行多少场次?
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:阅读理解
| 图形 | 直线上点的个数 | 共有线段条数 | 两者关系 | ||||
 |
2 | 1 | 1=0+1 | ||||
 |
3 | 3 | 3=0+1+2 | ||||
 |
4 | 6 | 6=0+1+2+3 | ||||
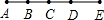 |
5 | 10 | 10=0+1+2+3+4 | ||||
| … | … | … | … | ||||
 |
n |
|
|
查看答案和解析>>
科目:初中数学 来源:2014湘教版七年级上册(专题训练 状元笔记)数学:第四章 图形的认识 几何图形 线段、射线、直线 湘教版 题型:044
通过阅读所得的启示,回答问题(阅读中的结论可以直接使用).
阅读:在直线上有n个不同的点,则此图中共有多少条线段?
通过画图尝试,我们发现了如下的规律:
问题:(1)某学校七年级共有8个班级进行辩论比赛,规定采用单循环赛制(每两个班之间赛一场),请问该校七年级的辩论赛共需进行多少场辩论赛?
(2)往返上海与北京之间的某趟火车,共有15个车站(包括上海与北京),则共需要准备多少种不同的车票?
查看答案和解析>>
科目:初中数学 来源:黄冈重点作业 初三数学(下) 题型:047
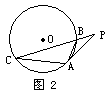
阅读:如图所示,△ABC内接于⊙O,∠CAE=∠B.

求证:AE与⊙O相切于点A.
证明:作直径AF,连结FC,则∠ACF= .
.
∴∠AFC+∠CAF=
∵∠B=∠AFC
∴∠B+∠CAF=
又∵∠CAE=∠B
∴∠CAE+∠CAF= .
.
即AE与⊙O相切于点A.
问题:通过阅读得到的启示证明下题(阅读中的结论可直接应用).
如图所示,已知△ABC内接于⊙O,P是CB延长线上一点,连结AP,且PA2=PB·PC.求证:PA是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 图形 | 直线上点的个数 | 共有线段条数 | 两者关系 |
 | 2 | 1 | 1=0+1 |
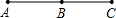 | 3 | 3 | 3=0+1+2 |
 | 4 | 6 | 6=0+1+2+3 |
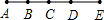 | 5 | 10 | 10=0+1+2+3+4 |
| … | … | … | … |
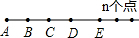 | n | 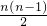 | 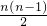 =0+1+2+3+…+(n-1) =0+1+2+3+…+(n-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com