
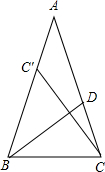
 如图,D是△ABC的边AC上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在一边上的C′处.
如图,D是△ABC的边AC上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在一边上的C′处.分析 (1)连接C'D,根据AB=AC,BD=BC,可得∠ABC=∠ACB=∠BDC,然后根据折叠的性质可得CD=C′D,BC′=BC,∠BCD=∠BC'D,继而得出∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,即可得出∴∠A=∠ABD=∠CBD,根据三角形外角的性质得出∠AC′D≠∠A,则AD≠C′D,根据等妖三角形三线合一的性质即可求得BD垂直平分CC′;
(2)根据四边形的内角和求出各角的度数,最后可求得∠A的大小.
解答 解:(1)连接C'D,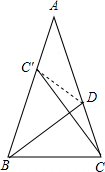
∵AB=AC,BD=BC,
∴∠ABC=∠ACB=∠BDC,故②正确;
∵△BCD沿BD折叠,顶点C恰好落在AB边的C′处,
∴CD=C′D,BC′=BC,故①正确;
∵∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,
∴∠A=∠ABD=∠CBD,
∵∠AC′D=∠ABD+∠BDC′,
∴∠AC′D≠∠A,
∴AD≠C′D,
∴CD≠AD,故③错误;
∵BC=BC′,∠CBD=∠C′BD,
∴BD垂直平分CC′,故④正确;
故①②④,
故答案为①②④;
(2)∵四边形BCDC'的内角和为360°,
∴∠ABC+∠BCD+∠BDC+∠BDC'+∠BC'D=360°,
∵∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,
∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D=$\frac{360°}{5}$=72°,
∴∠A=180°-∠ABC-∠ACB=36°.
点评 本题考查了折叠的性质,解答本题的关键是掌握翻折前后的对应角相等,注意本题的突破口在于得出∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,根据四边形的内角和为360°求出每个角的度数.


科目:初中数学 来源: 题型:解答题
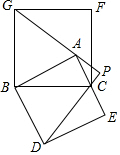 已知,△ABC中,∠BAC=90°,分别以AB、BC为边作正方形ABDE和正方形BCFG,延长DC、GA交于点P.
已知,△ABC中,∠BAC=90°,分别以AB、BC为边作正方形ABDE和正方形BCFG,延长DC、GA交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
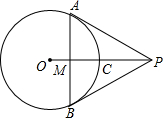 如图,PA,PB与⊙O相切于点A,B,连接AB,PO交⊙O于点C,交AB于点M.
如图,PA,PB与⊙O相切于点A,B,连接AB,PO交⊙O于点C,交AB于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
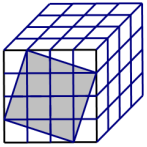 魔方,又叫魔术方块,也称鲁比克方块,是匈牙利布达佩斯建筑学院厄尔诺•鲁比克教授在1974年发明的.魔方与中国人发明的“华容道”,法国人发明的“独立钻石”一同被称为智力游戏界的三大不可思议.如图是一个4阶魔方,又称“魔方的复仇”,由四层完全相同的64个小立方体组成,体积为64cm3.
魔方,又叫魔术方块,也称鲁比克方块,是匈牙利布达佩斯建筑学院厄尔诺•鲁比克教授在1974年发明的.魔方与中国人发明的“华容道”,法国人发明的“独立钻石”一同被称为智力游戏界的三大不可思议.如图是一个4阶魔方,又称“魔方的复仇”,由四层完全相同的64个小立方体组成,体积为64cm3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com