练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，是二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴交于点为A（3，0），则由图象可知，方程ax2+bx+c的另一个解是（ ）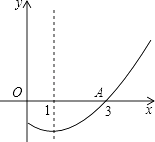
    A.﹣1
    B.﹣2
    C.﹣1.5
    D.﹣2.5

    【答案】A
    【解析】解：由抛物线的对称性得：抛物线的与x轴另一个交点为（﹣1，0）， ∴方程ax2+bx+c的另一个解为：x=﹣1，
    故选A．
    【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识，掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点P，Q是反比例函数y= 图象上的两点，PA⊥y轴于点A，QN⊥x轴于点N，作PM⊥x轴于点M，QB⊥y轴于点B，连接PB、QM，△ABP的面积记为S1 ， △QMN的面积记为S2 ， 则S1S2 ． （填“＞”或“＜”或“=”）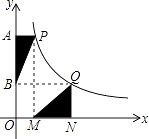

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，E，F分别是AC，BC边上一点．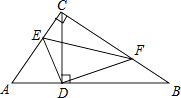
    （1）求证： ；
    （2）若CE= AC，BF= BC，求∠EDF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△OAB的顶点A，B的坐标分别为（4，0）、（4，n），若经过点O、A的抛物线y=﹣x2+bx+c的顶点C落在边OB上，则图中阴影部分图形的面积和为 ．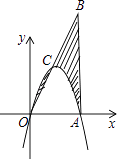

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l与x轴相交于点M（3，0），与y轴相交于点N（0，﹣1），反比例函数y= （x＞0）的图象经过线段MN的中点A．
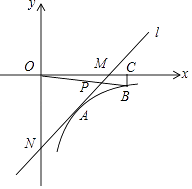
    （1）求直线l和反比例函数的解析式；
    （2）在函数y= （x＞0）的图象上取不同于点A的一点B，作BC⊥x轴于点C，连接OB交直线l于点P，若△ONP的面积是△OBC的面积的3倍，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在⊙O中，AB是⊙O的直径，AC是⊙O的弦，过点C作⊙O的切线交BA的延长线于点P，连接BC．
    （1）求证：∠PCA=∠B；
    （2）填空：已知∠P=40°，AB=12cm，点Q在 上，从点A开始以πcm/s的速度逆时针运动到点C停止，设运动时间为ts． ①当t=时，以点A、Q、B、C为顶点的四边形面积最大；
    ②当t=时，四边形AQBC是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为2，则图中阴影部分的面积为（结果保留π）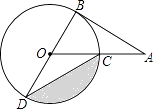

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．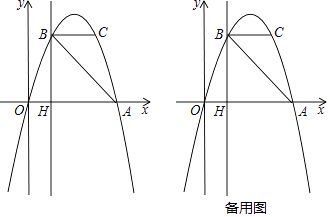
    （1）求抛物线的表达式；
    （2）直接写出点C的坐标，并求出△ABC的面积；
    （3）点P是抛物线上一动点，且位于第四象限，当△ABP的面积为6时，求出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程：x2﹣2（m+1）x+m2+5=0有两个不相等的实数根．
    （1）求m的取值范围；
    （2）若原方程的两个实数根为x1、x2 ， 且满足x12+x22=|x1|+|x2|+2x1x2 ， 求m的值．

    查看答案和解析>>

    同步练习册答案