���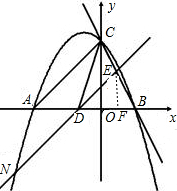
�⣺��1����x=0ʱ��y=4��
��C��0��4����1�֣�
��y=0ʱ��x=-4��
��A��-4��0����2�֣�
��Rt��AOC�У�OA=OC=4����AOC=90�㣬
��AC=
==4����3�֣�
��2���������߾�����A��C����
��
���
��
������������Ӧ�ĺ�����ϵʽΪ
y=-x2-x+4����4�֣�
�ߡ�CAD����ACΪ�ĵ��������Σ�
���D��AC�Ĵ�ֱƽ�����ϣ�
��ʱ��D��ԭ���غϣ���D��0��0������5�֣�
��m=OC=4��
��ƽ�ƺ��ֱ������Ӧ�ĺ�����ϵʽΪy=x����6�֣�
�ߵ�N��������
y=-x2-x+4��ֱ��y=x�Ľ��㣬
�����N��a��a����
��
a=-a2-a+4��
���a=
-2��2��
�ߵ�N�������߶Գ������࣬
��N��
-2-2��
-2-2������7�֣�
�����CDE�����ΪS��
��
y=-x2-x+4����y=0��
���x=-4��x=2��
��B��2��0����AB=6��
����D�ڵ�B�����ʱ������0��m��6ʱ����ͼ����
ƽ�ƺ��ֱ��Ϊy=x+4-m��
��y=0ʱ��x=m-4��
��D��m-4��0����
��BD=2-��m-4��=6-m����8�֣�
����E��EF��AB�ڵ�F��
��DE��AC���á�BDE=��CAD��
���BDE�ס�BAC��
��
=����
=��
���
EF=����9�֣�
��
S=S��BCD-S��BDE=•(6-m)��4-•(6-m)•=-m2+2m=
-(m-3)2+3��
�������ߵĿ������£��Գ���Ϊֱ��m=3��
�߶��㣨3��3���ĺ������ڷ�Χ0��m��6�ڣ�
�൱m=3��S�����ֵΪ3����10�֣�
����D�ڵ�B���Ҳ�ʱ������m��6ʱ����ͼ����
ƽ�ƺ��ֱ������Ӧ�ĺ�����ϵʽΪy=x+4-m��
��y=0ʱ��x=m-4��
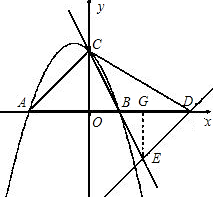
��D��m-4��0����
��BD=m-4-2=m-6��
����E��EG��AB�ڵ�G��
��DE��AC���á�BDE=��CAD��
���BDE�ס�BAC��
��
=����
=��
���
EG=����11�֣�
��
S=S��BCD+S��BDE=•(m-6)��4+•(m-6)•=m2-2m=
(m-3)2-3��
�������߿������ϣ��Գ���Ϊm=3��
���������߶Գ�����Ҳ࣬S����m�����������
�൱m��6ʱ��Sû�����ֵ����12�֣�
���ϵã���ֱ��ACƽ�ƵĹ����У�����mֵ����m=3��S�����ֵΪ3��ʹ�á�CDE��������13�֣�

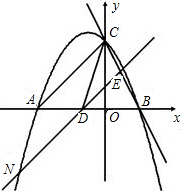 ��ֱ֪��y=x+4��y�ύ�ڵ�C����x�ύ�ڵ�A��
��ֱ֪��y=x+4��y�ύ�ڵ�C����x�ύ�ڵ�A�� �⣺��1����x=0ʱ��y=4��
�⣺��1����x=0ʱ��y=4��


 ������������ϵ�д�
������������ϵ�д�
 ��ͼ����ֱ֪��y=-x+4�뷴��������y=
��ͼ����ֱ֪��y=-x+4�뷴��������y=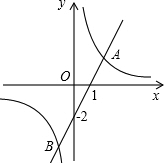 ��ֱ֪��y=2x-2��˫����ͼy=
��ֱ֪��y=2x-2��˫����ͼy=
 ��ͼ����ֱ֪��y1=x+m��y2=kx-1�ཻ�ڵ�P��-1��1���������x�IJ���ʽx+m��kx-1�Ľ⼯����
��ͼ����ֱ֪��y1=x+m��y2=kx-1�ཻ�ڵ�P��-1��1���������x�IJ���ʽx+m��kx-1�Ľ⼯����