解:(1)∵点A(1,m),B(2,n)在反比例函数图象上,
∴m=t,n=

t,
∵m=n+1,
∴t=

t+1,
解得t=2;
(2)x
2-2ax+a
2-1=0,
(x-a-1)(x-a+1)=0,
∴x-a-1=0,x-a+1=0,
解得x
1=a+1,x
2=a-1,
结合图形可知m>n,
∴m=a+1,n=a-1,
∴a+1=t,a-1=

t,
解得t=4,
∴反比例函数解析式为y=

,
∴点A、B的坐标是A(1,4)、B(2,2),
设直线AB的解析式为y=kx+b,
则
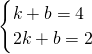
,
解得

,
∴直线AB的解析式为y=-2x+6,
当y=0时,-2x+6=0,
解得x=3,
∴点C的坐标为(3,0),
又∵A(1,4)、B(2,2),
∴AD=4,CD=3-1=2,且点B是AC的中点,
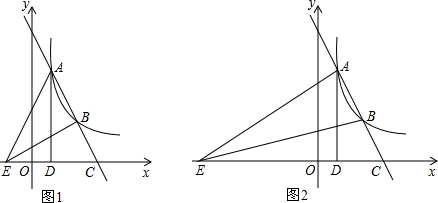
①如图1,当BE是直角边时,△AEC关于BE成轴对称,
∴∠AEB=∠CEB,
∵∠CEB+∠ACE=90°,∠CAD+∠ACD=90°,
∴∠CEB=∠AEB=∠CAD,
在△ABE与△CDA中,
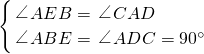
,
∴△ABE∽△CDA,
在Rt△CDA中,AC=

=

=2

,
∴BC=

AC=

,
∵∠ACD=∠ECB,∠ADC=∠EBC=90°,
∴△ACD∽△ECB,
∴

=
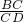
,
即
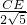
=

,
解得CE=5,
∴OE=3-5=-2,
∴点E的坐标为(-2,0),
②如图2,当AE是直角边时,∠ABE=∠BEC+∠ACD,
∴△ABE与△ADC不可能相似.
故在x轴上存在点E(-2,0),使得△ABE∽△CDA.
分析:(1)把点A、B的坐标代入反比例函数解析式,然后根据m=n+1代入整理得到关于t的一元一次方程,然后解方程即可得解;
(2)利用因式分解法求出方程的解,然后结合图形得到m、n的表达式,再根据(1)的方法利用反比例函数解析式代入求出t的值,从而得到点A、B的坐标,利用待定系数法求出直线AB的解析式,再求出点C的坐标,从而得到AD、CD的长度,然后分①BE是直角边时,利用两角对应相等,两三角形相似判定,再根据相似三角形对应边成比例列式求出CE的长,从而得到点E的坐标,②AE是直角边时,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ABE=∠BEC+∠ACD,从而得到△ABE与△ADC不可能相似.
点评:本题综合考查了反比例函数的问题,待定系数法求直线解析式,相似三角形的判定与性质,一元二次方程的求解,反比例函数图象与一次函数图象的交点问题,综合性质较强,难度较大.

 如图,已知点A(1,m),B(2,n)在反比例函数
如图,已知点A(1,m),B(2,n)在反比例函数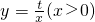 的图象,设直线AB与x轴交于点C,AD⊥x轴于D点,
的图象,设直线AB与x轴交于点C,AD⊥x轴于D点, t,
t, t+1,
t+1, t,
t, ,
,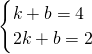 ,
, ,
,
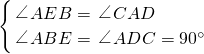 ,
, =
= =2
=2 ,
, AC=
AC= ,
, =
=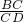 ,
,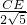 =
= ,
,

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设