
【题目】已知:如图,ABCD中,对角线AC、BD交于点O,直线EF经过点O,分别交DA,BC的延长线于点E,F,连接BE,DF. 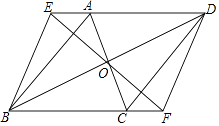
求证:
(1)AE=CF;
(2)四边形BEDF是平行四边形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠AEO=∠CFO,
∵∠AOE=∠COF,
∴△AOE≌△COF,
∴AE=CF

(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,
∵AE=CF,
∴AD+AE=BC+CF,
∴DE=BF,
∵DE∥BF,
∴四边形BEDF是平行四边形.
【解析】(1)只要证明△AOE≌△COF即可;(2)只要证明DE=BF,DE∥BF即可;
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
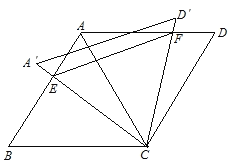
【题目】如图,菱形ABCD中,边长为2,∠B=60°,将△ACD绕点C旋转,当AC(即A′C)与AB交于一点E,CD(即CD′)同时与AD交于一点F时,点E,F和点A构成△AEF。试探究△AEF的周长是否存在最小值,如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com