
【题目】如图①所示,直线L:y=m(x+10)与x轴负半轴、y轴正半轴分别交于A、B两点.

(1)当OA=OB时,试确定直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=8,BN=6,求MN的长;
(3)当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图③.
问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值?若是,请求出其值;若不是,说明理由.
【答案】(1)y=x+10(2)14(3)PB的长为定值, PB=5
【解析】
试题分析:(1)令y=0可求得x=﹣10,从而可求得点A的坐标,令x=0得y=10m,由OA=OB可知点B的纵坐标为10,从而可求得m的值;
(2)依据AAS证明△AMO≌△ONB,由全等三角形的性质可知ON=AM,OM=BN,最后由MN=AM+BN可求得MN的长;
(3)过点E作EG⊥y轴于G点,先证明△ABO≌△EGB,从而得到BG=10,然后证明△BFP≌△GEP,从而得到BP=GP=![]() BG.
BG.
解:(1)由题意知:A(﹣10,0),B(0,10m)
∵OA=OB,
∴10m=10,即m=1.
∴L的解析式y=x+10.
(2)∵AM⊥OQ,BN⊥OQ
∴∠AMO=∠BNO=90°
∴∠AOM+∠MAO=90°
∵∠AOM+BON=90°
∴∠MAO=∠NOB
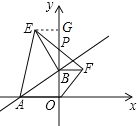
在△AMO和△ONB中,
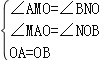 ,
,
∴△AMO≌△ONB.
∴ON=AM,OM=BN.
∵AM=8,BN=6,
∴MN=AM+BN=14.
(3)PB的长为定值.
理由:如图所示:过点E作EG⊥y轴于G点.
∵△AEB为等腰直角三角形,
∴AB=EB,∠ABO+∠EBG=90°.
∵EG⊥BG,
∴∠GEB+∠EBG=90°.
∴∠ABO=∠GEB.
在△ABO和△EGB中,
 ,
,
∴△ABO≌△EGB.
∴BG=AO=10,OB=EG
∵△OBF为等腰直角三角形,
∴OB=BF
∴BF=EG.
在△BFP和△GEP中,
 ,
,
∴△BFP≌△GEP.
∴BP=GP=![]() BG=5.
BG=5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在象限是( )
A.第一象限或第三象限 B.第二象限或第四象限
C.第一象限或第二象限 D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36000元购进甲、乙两种商品,销售完后共获利6000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学活动小组在一次活动中,对一个数学问题作如下探究:
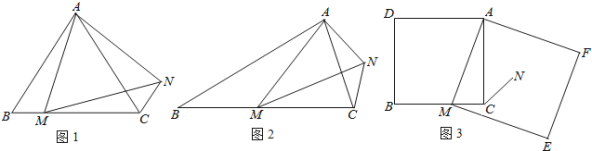
问题发现:如图1,在等边三角形ABC中,点M是边BC上任意一点,连接AM,以AM为边作等边三角形AMN,连接CN,证明:BM=CN.
变式探究:如图2,在等腰三角形ABC中,BA=BC,∠ABC=∠α,点M为边BC上任意一点,以AM为腰作等腰三角形AMN,MA=MN,使∠AMN=∠ABC,连接CN,请求出![]() 的值.(用含α的式子表示出来)
的值.(用含α的式子表示出来)
解决问题:如图3,在正方形ADBC中,点M为边BC上一点,以AM为边作正方形作AMEF,N为正方形AMEF的中心,连接CN,若正方形AMEF的边长为![]() ,CN=
,CN=![]() ,请你求正方形ADBC的边长.
,请你求正方形ADBC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点![]() 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决“最后一公里”的交通接驳问题,平谷区投放了大量公租自行车供市民使用.据统计,目前我区共有公租自行车3 500辆.将3 500用科学记数法表示应为( )
A. 0.35×104 B. 3.5×103 C. 3.5×102 D. 35×102
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com