
分析 (1)根据绝对值的性质可得a=±5,b=±2,根据(1)条件取得合适的a,b,再代入计算即可;
(2)根据(2)条件取得合适的a,b,再由绝对值的性质求得c,再代入计算即可;
解答 解:∵|a|=5,|b|=2,
∴a=±5,b=±2,
(1)∵a<0,b>0,
∴a=-5,b=2,
∴3a-2b=3×(-5)-2×2=-19;
(2)∵a>0,b<0,|c-2|=1,
∴a=5,b=-2,c=3或c=1,
当c=3时,2abc+|b-c|=2×5×(-2)3+|-2-3|=-80+5=-75;
当c=1时,2abc+|b-c|=2×5×(-2)+|-2-3|=-20+5=-15;
综上所述,2abc+|b-c|的值为-75或-15.
点评 本题主要考查了代数式求值,利用绝对值的定义解得a,b,c是解答此题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
 如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.
如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
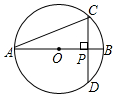 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$,
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
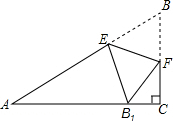 如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.
如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com