
【题目】如图所示,数轴上,点![]() 的初始位置表示的数为
的初始位置表示的数为![]() ,现点
,现点![]() 做如下移动,第1次点
做如下移动,第1次点![]() 向左移动3个单位长度至点
向左移动3个单位长度至点![]() ,第2次从点
,第2次从点![]() 向右移动6个单位长度至点
向右移动6个单位长度至点![]() ,第
,第![]() 次从点
次从点![]() 向左移动
向左移动![]() 个单位长度至点
个单位长度至点![]() ,…,按照这种移动方式进行下云,如果点
,…,按照这种移动方式进行下云,如果点![]() 与原点的距离不小于
与原点的距离不小于![]() ,那么
,那么![]() 的最小值是___.
的最小值是___.

【答案】13
【解析】
序号为奇数的点在点![]() 的左边,各点所表示的数依次减少3,序号为偶数的点在点
的左边,各点所表示的数依次减少3,序号为偶数的点在点![]() 的右侧,各点所表示的数依次增加3,于是可得到
的右侧,各点所表示的数依次增加3,于是可得到![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,则可判断点
,则可判断点![]() 与原点的距离不小于20时,
与原点的距离不小于20时,![]() 的最小值是13.
的最小值是13.
解:第一次点![]() 向左移动3个单位长度至点
向左移动3个单位长度至点![]() ,则
,则![]() 表示的数,1-3=-2;
表示的数,1-3=-2;
第2次从点![]() 向右移动6个单位长度至点
向右移动6个单位长度至点![]() ,则
,则![]() 表示的数为
表示的数为![]() ;
;
第3次从点![]() 向左移动9个单位长度至点
向左移动9个单位长度至点![]() ,则
,则![]() 表示的数为
表示的数为![]() ;
;
第4次从点![]() 向右移动12个单位长度至点
向右移动12个单位长度至点![]() ,则
,则![]() 表示的数为
表示的数为![]() ;
;
第5次从点![]() 向左移动15个单位长度至点
向左移动15个单位长度至点![]() ,则
,则![]() 表示的数为
表示的数为![]() ;
;
![]()
则![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,
![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,
所以点![]() 与原点的距离不小于20,那么
与原点的距离不小于20,那么![]() 的最小值是13.
的最小值是13.
故答案为:13.


科目:初中数学 来源: 题型:
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
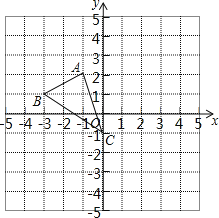
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:一般地,一个二元一次方程ax+by=c (a、b、c为常数,且a、b均不为0)有无数组解,我们规定:将其每一个解中x、y的值分别作为一个点的横、纵坐标描点在平面直角坐标系中,这样我们就得到了二元一次方程的图像:一条直线。即二元一次方程的解均满足其对应直线上点的坐标:反之直线上点的坐标均为其对应的二元一次方程的解。如2x -y = 0其中一解x=1,y=2则对应其图像上一点(1,2).
(1)如图,4x+3y=12的图像为直线m,其与x轴交点A的坐标为 ;其 与 y轴交点B的坐标为 ;
(2如图,ax+by=﹣5的图像为直线n,其与x轴交于C(![]() ,0),与(1)中直线m交于P,若点P的横坐标为1 ,求a和b的值.
,0),与(1)中直线m交于P,若点P的横坐标为1 ,求a和b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交点为O,正方形OEFG的边长与正方形ABCD的边长相等,若将正方形OEFG绕点O旋转,试说明旋转到如图的位置时,两正方形重叠部分的面积与正方形面积之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形OABC放入平面直角坐标系xO中,使OA、OC分别落在x、y轴的正半轴上,其中AB=15,对角线AC所在直线解析式为y=﹣![]() x+b,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.
x+b,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.
(1)求点B的坐标;
(2)求EA的长度;
(3)点P是y轴上一动点,是否存在点P使得△PBE的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
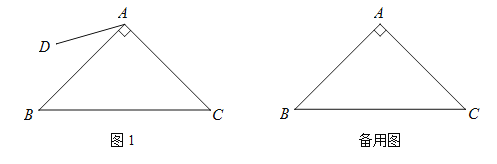
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
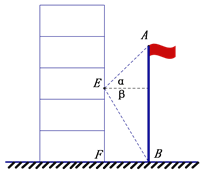
【题目】数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°. 室外测量组测得BF的长度为5米.则旗杆AB=______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强从A处出发沿北偏东70°方向行走,走至B处,又沿着北偏西30°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
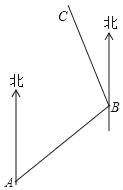
A. 左转 80° B. 右转80° C. 右转 100° D. 左转 100°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com