
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.
(1)如图1,当点 ![]() 与
与 ![]() 重合时,求证:四边形
重合时,求证:四边形 ![]() 是平行四边形;
是平行四边形;
(2)如图2,当点 ![]() 不与
不与 ![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 ![]() 交
交 ![]() 于点
于点 ![]() ,若
,若 ![]() ,且
,且 ![]() .
.
①求 ![]() 的度数;
的度数;
②当 ![]() ,
, ![]() 时,求
时,求 ![]() 的长.
的长.
【答案】
(1)
证明:∵DE//AB,∴∠EDC=∠ABM,
∵CE//AM,
∴∠ECD=∠ADB,
又∵AM是△ABC的中线,且D与M重合,∴BD=DC,
∴△ABD△EDC,
∴AB=ED,又∵AB//ED,
∴四边形ABDE为平行四边形。
(2)
解:结论成立,理由如下:
过点M作MG//DE交EC于点G,
∵CE//AM,
∴四边形DMGE为平行四边形,
∴ED=GM且ED//GM,
由(1)可得AB=GM且AB//GM,
∴AB=ED且AB//ED.
∴四边形ABDE为平行四边形.

(3)
解:①取线段HC的中点I,连结MI,
∴MI是△BHC的中位线,
∴MI//BH,MI=![]() BH,
BH,
又∵BH⊥AC,且BH=AM,
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°
②设DH=x,则AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,∴BH=4+2x,
由(2)已证四边形ABDE为平行四边形,
∴FD//AB,
∴△HDF~△HBA,
∴![]() ,即
,即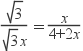
解得x=1±![]() (负根不合题意,舍去)
(负根不合题意,舍去)
∴DH=1+![]() .
.

【解析】(1)由DE//AB,可得同位角相等:∠EDC=∠ABM,由CE//AM,可得同位角相等∠ECD=∠ADB,又由BD=DC,则△ABD△EDC,得到AB=ED,根据有一组对边平行且相等,可得四边形ABDE为平行四边形.
(2)过点M作MG//DE交EC于点G,则可得四边形DMGE为平行四边形,且ED=GM且ED//GM,由(1)可得AB=GM且AB//GM,即可证得;
(3)①在已知条件中没有已知角的度数时,则在求角度时往特殊角30°,60°,45°的方向考虑,则要求这样的特殊角,就去找边的关系,构造直角三角形,取线段HC的中点I,连结MI,则MI是△BHC的中位线,可得MI//BH,MI=![]() BH,且MI⊥AC,则去找Rt△AMI中边的关系,求出∠CAM;
BH,且MI⊥AC,则去找Rt△AMI中边的关系,求出∠CAM;
②根据①所得的∠CAM,则可设DH=x,即可用x分别表示出AH=![]() x,AD=2x,AM=4+2x,BH=4+2x,由△HDF~△HBA,得到对应边成比例,求出x的值即可;
x,AD=2x,AM=4+2x,BH=4+2x,由△HDF~△HBA,得到对应边成比例,求出x的值即可;
【考点精析】认真审题,首先需要了解三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半),还要掌握平行四边形的判定与性质(若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】两根木棒分别为5cm和7cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒长为偶数,则方法有( )
A.3种B.4种C.5种D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.用一个平面去截一个圆锥,可以是椭圆
B.棱柱的所有侧棱长都相等
C.用一个平面去截一个圆柱体,截面可以是梯形
D.用一个平面去截一个长方体截面不能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房200间供游客居住,当每间客房的定价为每天180元时,客房恰好全部住满;如果每间客房每天的定价每增加10元,就会减少4间客房出租.设每间客房每天的定价增加 ![]() 元,宾馆出租的客房为
元,宾馆出租的客房为 ![]() 间.求:
间.求:
(1)![]() 关于
关于 ![]() 的函数关系式;
的函数关系式;
(2)如果某天宾馆客房收入38400元,那么这天每间客房的价格是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com