
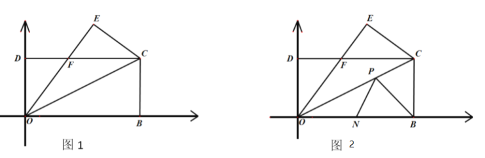
【题目】如图,长方形![]() 的
的![]() 边在
边在![]() 轴上,
轴上,![]() 边在
边在![]() 轴上.把
轴上.把![]() 沿
沿![]() 折叠得到
折叠得到![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)如图1,求证:![]() .
.
(2)如图1,若![]() ,
,![]() .写出
.写出![]() 所在直线的解析式.
所在直线的解析式.
(3)如图2,在(2)的条件下,![]() 是
是![]() 中点,
中点,![]() 是直线
是直线![]() 上一动点,
上一动点,![]() 是否有最小值,若有请求出最小值,若没有请说明理由.
是否有最小值,若有请求出最小值,若没有请说明理由.
【答案】(1)见解析;(2)![]() ;(3)有最小值,最小值是
;(3)有最小值,最小值是![]()
【解析】
(1)先依据翻折的性质、矩形的性质证明∠COB=∠COE,∠FCO=∠COB,利用等角对等边即可得到结论;
(2)在Rt△ODF中,依据勾股定理可求得DF的长,从而可得到点F的坐标,然后根据待定系数法即可求得;
(3)由翻折的性质可知点B与点E关于直线OC对称,连接EN交OC于点P,此时PB+PN有最小值,最小值是线段EN,利用勾股定理即可求解.
(1)∵四边形OBCD为矩形,
∴CD∥BO,
∴∠FCO=∠COB,
由翻折的性质可知∠COB=∠COE,
∴∠FCO =∠COE,
∴OF=CF;
(2)∵OF=CF,![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,
在Rt△ODF中,OD=4,根据勾股定理得,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴点F的坐标为(3,4),
设直线OE的解析式为![]() ,
,
把F(3,4)代入得:![]() ,
,
∴![]() ,
,
∴OE所在直线的解析式为:![]() ;
;
(3)有最小值,理由如下:
由翻折的性质可知点B与点E关于直线OC对称,连接EN交OC于点P,此时PB+PN有最小值,最小值是线段EN,

由翻折的性质可知OE=OB=8,
∵点E在直线![]() 上,
上,
∴设点E的坐标为![]() ,
,
在Rt△OEG中,OE=8,OG=![]() ,EG=
,EG=![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴OG=![]() ,EG=
,EG=![]() ,
,
∵![]() 是
是![]() 中点,
中点,
∴ON=![]() ,
,
∴NG= OG- ON=![]() ,
,
在Rt△NEG中,![]() ,
,![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A—C—B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C—B—A向A点运动,当其中一点运动到终点时,两点同时停止运动。设运动时间为t秒,当t=_______秒时,△PCQ的面积等于8cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
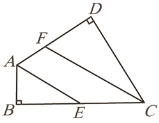
【题目】如图,已知四边形ABCD中,∠D=∠B=90°.
(1)填空:∠DAB+∠BCD= °;
(2)若AE平分∠DAB,CF平分∠BCD,求证:AE∥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,边长为1的正方形网格中,![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 都在格点上.
都在格点上.
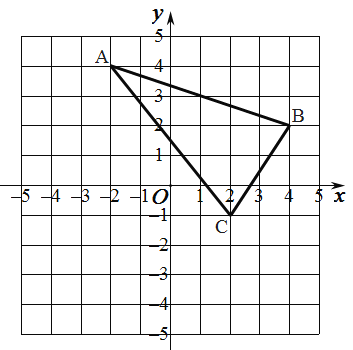
(1)作关于![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,(其中
,(其中![]() 、
、![]() 、
、![]() 的对称点分别是
的对称点分别是![]() 、
、![]() 、
、![]() ),并写出点
),并写出点![]() 坐标;
坐标;
(2)![]() 为
为![]() 轴上一点,请在图中画出使
轴上一点,请在图中画出使![]() 的周长最小时的点
的周长最小时的点![]() (不写画法,保留画图痕迹),并直接写出点
(不写画法,保留画图痕迹),并直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.

(1)求证:DA∥BC;
(2)猜想线段DF、AF的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿矩形的边由![]() 运动,设点P运动的路程为x,
运动,设点P运动的路程为x,![]() 的面积为y,把y看作x的函数,函数的图像如图2所示,则
的面积为y,把y看作x的函数,函数的图像如图2所示,则![]() 的面积为( )
的面积为( )

A. 10 B. 16 C. 18 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售樱桃,已知樱桃的进价为15元/千克,如果售价为20元/千克,那么每天可售出250千克,如果售价为25元/千克,那么每天可售出200千克,经调查发现:每天的销售量y(千克)与售价x(元/千克)之间 存在一次函数关系.
(1)求y与x之间的函数关系式;
(2)若该超市每天要获得利润810元,同时又要让消费者得到实惠,则售价x应定于多少元?
(3)若樱桃的售价不得高于28元/千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形则组成的三角形的周长( )
A.最小值是11B.最小值是12C.最大值是14D.最大值是15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com