
����Ŀ��һ�п쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ��������������ʻ��ʱ��Ϊx(h)������֮��ľ���Ϊy(km)��ͼ�е����߱�ʾy��x֮��ĺ�����ϵ����������������Ϣ����������⣺
(1)�ס�������֮��ľ���Ϊ____km��ͼ�е�C��ʵ������Ϊ��______���������ٶ�Ϊ_______���쳵���ٶ�Ϊ______��
(2)���߶�BC����ʾ��y��x֮��ĺ�����ϵʽ���Լ��Ա���x��ȡֵ��Χ��
(3)���ڵ�һ�п쳵����������ʱ���ڶ��п쳵���ҵس���ʻ���أ��ٶ����һ�п쳵��ͬ����ֱ��д���ڶ��п쳵�����ʱ�䣬���������200km��
(4)�������п쳵Ҳ���ҵس���ʻ���أ��ٶ����һ�п쳵��ͬ����������п쳵���ܱ�����������������п쳵�������������������Сʱ��

���𰸡�(1)960����������ʻ6 hʱ���쳵�����ҵأ�80km/h��160km/h��(2)y��240x��960(4��x��6)��(3)�ڶ��п쳵����1.5h�����������200km��(4)�����п쳵���������������6Сʱ��
��������
��1������ͼ�ɿ�����������֮��ľ��룬����ͼ��֪��������ʻ��ʱ����12h���쳵��ʻ��ʱ����6h�������ٶȹ�ʽ����ٶȼ��ɣ�
��2�����߶�BC����ʾ��y��x֮��ĺ�����ϵʽΪy=kx+b����������ʾ���������B��C�����꣬����������ɣ�
��3����Ϊ�������������ڶ��п쳵����ah�����������200km����������ó�����4��80+80a-200=160a��������ɣ�
�ڵڶ��п����������Ժ��ٳ�������200km����ڶ��п쳵����ah�����������200km����160a-80a=4��80+200��������ɣ�
��4��������п쳵����������t h��������ó�����ʽt+![]() ��
��![]() ���������ʽ�Ľ⼯���ɣ�
���������ʽ�Ľ⼯���ɣ�
�⣺(1)��ͼ���֪���ס�������֮��ľ�����960km��
ͼ�е�C��ʵ�������ǣ���������ʻ6 hʱ���쳵�����ҵأ�
�������ٶ��ǣ�960km��12h��80km/h��
�쳵���ٶ��ǣ�960km��6h��160km/h��
�ʴ�Ϊ��960����������ʻ6 hʱ���쳵�����ҵأ�80km/h��160km/h��
(2)�������⣬������ʻ960km����������ʱ��![]() ��4(h)��
��4(h)��
���Ե�B������Ϊ(4��0)����Сʱ�������2��(160+80)��480(km)��
���Ե�C������Ϊ(6��480)��
���߶�BC����ʾ��y��x֮��ĺ�����ϵʽΪy��kx+b����(4��0)��(6��480)�����![]() ��
��
���![]() ��
��
���ԣ��߶�BC����ʾ��y��x֮��ĺ�����ϵʽΪy��240x��960���Ա���x��ȡֵ��Χ��4��x��6��
(3)��Ϊ�������������ڶ��п쳵����ah�����������200km��
��4��80+80a��200��160a��
��ã�a��1.5��
���ڶ��п쳵����1.5h�����������200km��
�ڵڶ��п����������Ժ��ٳ�������200km��
��ڶ��п쳵����ah�����������200km��
��160a��80a��4��80+200����a��6.5��6��(��Ϊ�쳵����ؽ���6Сʱ������a��6.5��ȥ)
�ۺ�����������ó����ڶ��п쳵����1.5h�����������200km��
(4)������п쳵����������t h�������
��t+![]() ��
��![]() ��
��
��ã�t��6��
�ʵ����п쳵���������������6Сʱ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
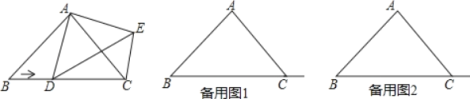
����Ŀ����3�֣���ͼ��AD����ABC�Ľ�ƽ���ߣ�DE��AC������ΪE��BF��AC��ED���ӳ����ڵ�F����BCǡ��ƽ����ABF��AE=2BF�����������ĸ����ۣ���DE=DF����DB=DC����AD��BC����AC=3BF��������ȷ�Ľ��۹��У� ��

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������̣�
��֪��DE��AO��E��BO��AO����CFB����EDO.
֤����CF��DO.

֤������DE��AO��BO��AO(��֪)
���DEA����BOA��90��(�� ��)
��DE��BO(�� )
���EDO����DOF(�� ��)
�֡ߡ�CFB����EDO(�� �� ��)
���DOF����CFB(�� �� ��)
��CF��DO(�� �� ��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ֱ֪��y����![]() x+4��x�ᡢy��ֱ���A��B���㣬��C(0��n)��y����һ�㣮������ƽ����ֱ��AC�۵���ʹ��B�պ�����x���ϣ����C������Ϊ______��
x+4��x�ᡢy��ֱ���A��B���㣬��C(0��n)��y����һ�㣮������ƽ����ֱ��AC�۵���ʹ��B�պ�����x���ϣ����C������Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ѵ���Rt��ABC�У���BAC��90������D�ӵ�B����������BC�ƶ�����ADΪ��������Rt��ADE����DAE��90��������CE��
(1)��ͼ����֤����ACE�ա�ABD��
(2)��D�˶�ʱ����BCE�Ķ����Ƿ����仯�������仯�������Ķ��������仯��˵�����ɣ�
(3)��AC��![]() ����CD��1ʱ����ֱ��д��DE�ij���
����CD��1ʱ����ֱ��д��DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��Ԫ���ڼ䣬ij���д��������棬���±���ʾ��
һ����������Ʒ��ԭ�� | �Żݰ취 |
������200Ԫ | û���Ż� |
����200Ԫ����������600Ԫ | ȫ���������Ż� |
����600Ԫ | ����600Ԫ�������Żݣ�����600Ԫ���ְ�8���Ż� |
��1��С��һ���Թ�����Ʒ��ԭ��Ϊ400Ԫ����ʵ�ʸ���Ϊ Ԫ��
��2��С������ʱһ���Ը���580Ԫ����������Ʒ��ԭ���Ƕ���Ԫ��
��3��С�Ժ�С��ֱ�ǰ���ó��й�����˸���������Ʒ��ԭ��֮��Ϊ1200Ԫ����С��������Ʒ��ԭ�۸���С�ԣ�����ʵ�ʸ��1074Ԫ����С�Ժ�С�����������Ʒ��ԭ�۷ֱ��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ѧ����չ�����������ÿ����5��ѧ���μӣ��������ֶܷ����������Σ�ͳ�Ʒ��ֳɼ���õļװ���Ұ��ܷ���ȣ��±��Ǽװ���Ұ�ѧ���ı�������![]() ��λ����
�����![]()
ѡ�� | 1�� | 2�� | 3�� | 4�� | 5�� | �ܼ� |
�װ� | 100 | 98 | 105 | 94 | 103 | 500 |
�Ұ� | 99 | 100 | 95 | 109 | 97 | 500 |
��ʱ��ѧ�����飬����ͨ�����������е�������Ϣ��Ϊ�ο��������������⣺
![]() ��������������е���λ�����Լ����
��������������е���λ�����Լ����
![]() ������������ݣ�˵��Ӧ�ö���һ����Ϊ�ھ���Ϊʲô��
������������ݣ�˵��Ӧ�ö���һ����Ϊ�ھ���Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����Σ�AB��4���ҡ�ABC����ABE��60�㣬MΪ�Խ���BD������B�㣩������һ�㣬��BM�Ƶ�B��ʱ����ת60��õ�BN������EN��AM��CM����AM+BM+CM����СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü����ֳ��Ŀ�С�����Σ�Ȼ��ͼ�ڵ���״ƴ��һ�������Σ�
(1)������ֲ�ͬ�ķ�����ͼ������Ӱ���ֵ������
����1��__����2��___
(2)�۲�ͼ������д��������������ʽ��![]() mn֮��ĵ�����ϵ��
mn֮��ĵ�����ϵ��
(3)����(2)���еĵ�����ϵ������������⣺
����֪��![]() ��
��![]() ��ֵ��
��ֵ��
����֪��![]() ����
����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com