
【题目】如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是( ) 
A.∠DAE=∠CBE
B.△DEA不全等于△CEB
C.CE=DE
D.△EAB是等腰三角形
【答案】B
【解析】解:∵∠1+∠C+∠ABC=∠2+∠D+∠DAB=180°,且∠1=∠2,∠C=∠D, ∴∠ABC=∠DAB,
∴∠ABC﹣∠2=∠DAB﹣∠1,
∴∠DAB=∠CBA.故A正确;
在△DEA和△CEB中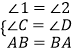 ,
,
∴△DEA≌△CEB(AAS),故B错误;
∴AC=BD.
∵∠1=∠2,
∴BE=AE,
∴△EAB是等腰三角形,AC﹣AE=BD﹣BE,故D正确;
∴CE=DE.故C正确.
故选B.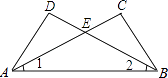
根据三角形的内角和定理就可以求出∠DAB=∠CBA,由等式的性质就可以得出∠DAE=∠CBE,根据AAS就可以得出△DEA≌△CEB;由△DEA≌△CEB就可以得出CE=DE,∠1=∠2就可以得出AE=BE,就可以得出结论.


科目:初中数学 来源: 题型:
【题目】某学校九年级8班10名学生积极奉献爱心,自发组织捐款,支援贫困山区儿童,若他们捐款的数额分别是(单位:元):10,15,20,10,5,15,10,5,10,5,则这组捐款的众数和中位数分别是( )
A.5元、10元
B.15元、5元
C.10元、15元
D.10元、10元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
∵ ![]() <
< ![]() <
< ![]() ,即2<
,即2< ![]() <3.
<3.
∴1< ![]() ﹣1<2
﹣1<2
∴ ![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴ ![]() ﹣1的小数部分为
﹣1的小数部分为 ![]() ﹣2.
﹣2.
解决问题:
已知a是 ![]() ﹣3的整数部分,b是
﹣3的整数部分,b是 ![]() ﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC和△DBE均为等腰直角三角形. 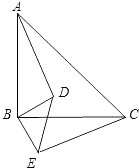
(1)求证:AD=CE;
(2)猜想:AD和CE是否垂直?若垂直,请说明理由;若不垂直,则只要写出结论,不用写理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=6,AC=4,BC=5.
(1)如图1,若AD是∠BAC的平分线,DE∥AB,求CE的长与 ![]() 的比值;
的比值; 
(2)如图2,将边AC折叠,使得AC在AB边上,折痕为AM,再将边MB折叠,使得MB'与MC'重合,折痕为MN,求AN的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有2个,黑球有1个,绿球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( ) 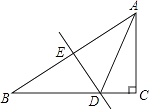
A.6
B.6 ![]()
C.9
D.3 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com