
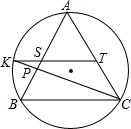
 正△ABC中与BC平行的中位线和△ABC的外接圆弧AB交于K,CK和AB交于P,求$\frac{AP}{BP}$.
正△ABC中与BC平行的中位线和△ABC的外接圆弧AB交于K,CK和AB交于P,求$\frac{AP}{BP}$. 分析 延长KT交△ABC的外接圆于G.设AB=BC=AC=2a,KS=TG=b,由SA•SB=KS•SG,列出方程求出b=$\frac{\sqrt{5}-1}{2}\\;a$a,再根据KG∥BC,得$\frac{KS}{BC}$=$\frac{SP}{PB}$,得$\frac{\frac{\sqrt{5}-1}{2}a}{2a}$=$\frac{SP}{a-SP}$,求出SP、PA、PB即可解决问题.
解答 解:如图, 延长KT交△ABC的外接圆于G.设AB=BC=AC=2a,KS=TG=b,
延长KT交△ABC的外接圆于G.设AB=BC=AC=2a,KS=TG=b,
∵ST是△ABC的中位线,
∴ST∥BC,AS=BS=a,
∵SA•SB=KS•SG,
∴a2=b(b+a),
∴b2+ab-a2=0,
∴b=$\frac{\sqrt{5}-1}{2}$a,
∵KG∥BC,
∴$\frac{KS}{BC}$=$\frac{SP}{PB}$,
∴$\frac{\frac{\sqrt{5}-1}{2}a}{2a}$=$\frac{SP}{a-SP}$,
∴SP=($\sqrt{5}-2$)a,AP=($\sqrt{5}$-1)a,PB=(3-$\sqrt{5}$)a,
∴$\frac{AP}{BP}$=$\frac{(\sqrt{5}-1)a}{(3-\sqrt{5})a}$=$\frac{\sqrt{5}+1}{2}$.
点评 本题考查等边三角形的性质.三角形的外接圆外心、三角形的中位线定理等知识,解题的关键是学会利用参数,构建方程解决问题,属于中考常考题型.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
 如图1,直角三角形ABE,∠AEB=90°,∠BAE=30°,以AB为边作菱形ABCD,∠DAB=60°,点Q从A出发,沿折线AD-DC运动,运动到点C停止,设点Q运动的时间为t(s).△AEQ的面积s(cm2)与t(s)之间函数关系的图象由图2中的线段OP、PF给出.
如图1,直角三角形ABE,∠AEB=90°,∠BAE=30°,以AB为边作菱形ABCD,∠DAB=60°,点Q从A出发,沿折线AD-DC运动,运动到点C停止,设点Q运动的时间为t(s).△AEQ的面积s(cm2)与t(s)之间函数关系的图象由图2中的线段OP、PF给出.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
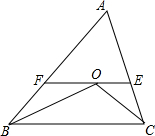 如图,△ABC中,BO,CO分别为∠ABC,∠ACB的平分线.交点为O,过O作EF平行于BC交AB,AC于F,E,探索BF+CE与FE的关系.说明理由.
如图,△ABC中,BO,CO分别为∠ABC,∠ACB的平分线.交点为O,过O作EF平行于BC交AB,AC于F,E,探索BF+CE与FE的关系.说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,P为⊙O外一点,OP⊥弦AB,PA与⊙O相切于点A,BC∥OP,交⊙O于点C.若OC=2,OP=$\frac{7}{2}$,求弦AB的长.
如图,P为⊙O外一点,OP⊥弦AB,PA与⊙O相切于点A,BC∥OP,交⊙O于点C.若OC=2,OP=$\frac{7}{2}$,求弦AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com