
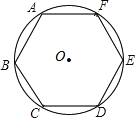
【题目】如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是 .
【答案】![]() .
.
【解析】
试题分析:连接OE、OD,由正六边形的特点求出判断出△ODE的形状,作OH⊥ED于H,由特殊角的三角函数值求出OH的长,利用三角形的面积公式即可求出△ODE的面积,进而可得出正六边形ABCDEF的面积,即可得出结果.
解:设⊙O的半径为R,连接OE、OD,如图所示:

∵六边形ABCDEF是正六边形,
∴∠DEF=120°,
∴∠OED=60°,
∵OE=OD=R,
∴△ODE是等边三角形,
∴DE=OD=R,
作OH⊥ED于H,则OH=OEsin∠OED=R×![]() =
=![]() R,
R,
∴S△ODE=![]() DEOH=
DEOH=![]() ×R×
×R×![]() =
=![]() R2,
R2,
∴正六边形的面积=6×![]() R2=
R2=![]() R2,
R2,
∵⊙O的面积=πR2,
∴所投的点落在正六边形ABCDEF内的概率=![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
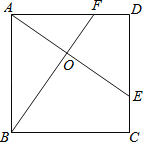
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A. 对角线互相平分且相等的四边形是正方形
B. 对角线互相平分的四边形是平行四边形
C. 对角线相等的四边形是矩形
D. 对角线互相垂直的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技运动会.下图为我市某校2009年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:
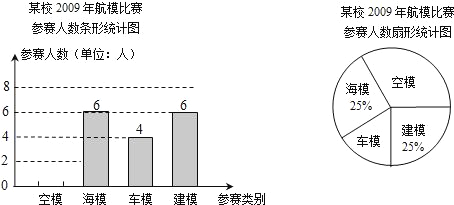
(1)该校参加车模、建模比赛的人数分别是 人和 人;
(2)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 °,并把条形统计图补充完整;(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑)
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖.今年我市中小学参加航模比赛人数共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,二次函数y=ax2﹣2ax+c(a>0)的图象与y轴交于点C(0,﹣4),与x轴交于点A、B两点,点A的坐标为(4,0).

(1)求该抛物线的函数解析式;
(2)点P(t,0)是线段OB上一动点(不与O、B重合),点E是线段BC上的点,以点B、P、E为顶点的三角形与三角形ABC相似,连结CP,求△CPE的面积S与t的函数关系式;
(3)如图2,若平行于x轴的动直线与该抛物线交于点Q,与直线AC交于点F,点D的坐标为(2,0),则存在这样的直线,使得△ODF为等腰三角形,请直接写出点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀将其均分成四块小长方形,然后按图②的形状拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于__________.
(2)请用两种不同的方法求图②中阴影部分的面积.
方法1:__________ ;
方法2:__________ .
(3)观察图②,你能写出代数式:(m+n)2,(m-n)2,mn之间的等量关系吗?
_______________________ _ .
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,则(a-b)2=___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.

(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com