
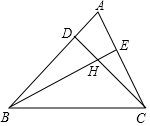
 如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.分析 (1)欲求∠BHC,根据∠BHC=180°-∠HBC-∠HCB,只要求出∠HBC,∠HCB即可;
(2)解法类似(1);
解答 解:(1)∵BE⊥AC,∠ACB=70°,
∴∠EBC=90°-70°=20°,
∵CD⊥AB,∠ABC=40°,
∴∠DCB=90°-40°=50°,
∴∠BHC=180°-20°-50°=110°.
(2)∵BE平分∠ABC,∠ABC=40°,
∴∠EBC=20°,
∵DC平分∠ACB,∠ACB=70°,
∴∠DCB=35°,
∴∠BHC=180°-20°-35°=125°
点评 本题考查三角形内角和定理、三角形的高、角平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考基础题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
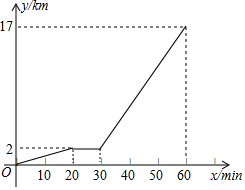 星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题:
星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.186×103 | B. | 3.186×104 | C. | 31.86×102 | D. | 0.3186×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com