
 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.分析 [发现与证明]由平行四边形的性质得出∠EAC=∠ACB,由翻折的性质得出∠ACB=∠ACB′,证出∠EAC=∠ACB′,得出AE=CE;得出DE=B′E,证出∠CB′D=∠B′DA=$\frac{1}{2}$(180°-∠B′ED),由∠AEC=∠B′ED,得出∠ACB′=∠CB′D,即可得出B′D∥AC;
[应用与探究]:分两种情况:①由正方形的性质得出∠CAB′=90°,得出∠BAC=90°,再由三角函数即可求出AC;
②由正方形的性质和已知条件得出AC=BC=2.
解答 解:[发现与证明]:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠EAC=∠ACB,
∵△ABC≌△AB′C,
∴∠ACB=∠ACB′,BC=B′C,
∴∠EAC=∠ACB′,
∴AE=CE,
即△ACE是等腰三角形;
∴DE=B′E,
∴∠CB′D=∠B′DA=$\frac{1}{2}$(180°-∠B′ED),
∵∠AEC=∠B′ED,
∴∠ACB′=∠CB′D,
∴B′D∥AC;
[应用与探究]:分两种情况:①如图1所示: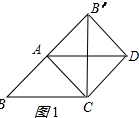 ∵四边形ACDB′是正方形,
∵四边形ACDB′是正方形,
∴∠CAB′=90°,
∴∠BAC=90°,
∵∠B=45°,
∴AC=$\frac{\sqrt{2}}{2}$BC=$\sqrt{2}$;
②如图2所示: AC=BC=2;
AC=BC=2;
综上所述:AC的长为$\sqrt{2}$或2.
点评 本题考查了平行四边形的性质、正方形的性质、翻折变换、等腰三角形的判定以及平行线的判定;熟练掌握平行四边形的性质、翻折变换的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
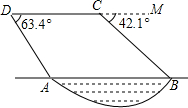 如图,某勘测飞机为了测量一湖泊两端A、B的距离,飞机在距离湖面垂直高度为90米的点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.
如图,某勘测飞机为了测量一湖泊两端A、B的距离,飞机在距离湖面垂直高度为90米的点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
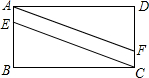 如图,在?ABCD中,E、F分别为边AB、CD上的点,且AE=$\frac{1}{5}$AB,CF=$\frac{1}{5}$CD,求证:四边形AECF是平行四边形.
如图,在?ABCD中,E、F分别为边AB、CD上的点,且AE=$\frac{1}{5}$AB,CF=$\frac{1}{5}$CD,求证:四边形AECF是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com