
 .
.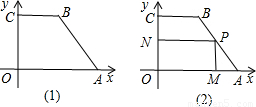
 ,得到MA=
,得到MA= x,由矩形的面积,可求出y与x之间的函数关系式;
x,由矩形的面积,可求出y与x之间的函数关系式; S梯形OABC可得到一点;
S梯形OABC可得到一点; 解:(1)由图得,A(6,0),B(3,4),C(0,4),
解:(1)由图得,A(6,0),B(3,4),C(0,4), 得,
得, x,
x, x)x,
x)x, +6x;
+6x; +6x(0<x<4);
+6x(0<x<4); +6x=
+6x= ×[(3+6)×4÷2]整理得,
×[(3+6)×4÷2]整理得, =
= ,
, ,2).
,2).

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012学年人教版中考数学第一轮复习一元一次方程专项训练 题型:解答题
(2011江苏连云港,21,6分)根据我省“十二五”铁路规划,连云港至徐州客运专线项目建成后,连云港至徐州的最短客运时间将由现在的2小时18分钟缩短为36分钟,其速度每小时将提高260km,求提速后的火车速度.(精确到1km/h)
查看答案和解析>>
科目:初中数学 来源:2009年江苏省南京市中考数学模拟卷(解析版) 题型:解答题
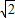 ≈1.41,
≈1.41,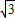 ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源:2009年湖南省衡阳市常宁市胜桥中学中考数学模拟测试卷(解析版) 题型:解答题
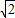 ≈1.41,
≈1.41, ≈1.73)
≈1.73)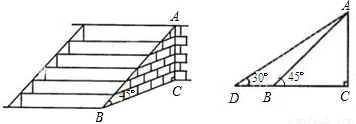
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com