
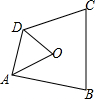
 如图,O为四边形ABCD内的一点,且AO,DO分别平分∠BAD,∠ADC,已知∠B+∠C=150°,求∠AOD的度数.
如图,O为四边形ABCD内的一点,且AO,DO分别平分∠BAD,∠ADC,已知∠B+∠C=150°,求∠AOD的度数. 分析 根据四边形的内角和定理,可得(∠BAD+∠CDA)的度数,根据角平分线的定义,可得(∠ADO+∠DAO)的度数,根据三角形的内角和定理,可得答案.
解答 解:由四边形的内角和,得
∠BAD+∠CDA=360°-(∠B+∠C)=360°-150°=210°,
由AO,DO分别平分∠BAD,∠ADC,得
∠ADO+∠DAO=$\frac{1}{2}$(∠BAD+∠CDA)=$\frac{1}{2}$×210°=$\frac{210°}{2}$=105°,
由三角形的内角和,得
∠AOD=180°-(∠ADO+∠DAO)=180°-105°=75°.
点评 本题考查了多边形内角与外角,利用四边形内角和得出(∠BAD+∠CDA)的度数,又利用了三角形的内角和定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{1{3}^{2}{-5}^{2}}$=13-5=8 | B. | $\sqrt{4}$=±2 | ||
| C. | $\sqrt{(-9)×(-25)}$=$\sqrt{(-9)}$×$\sqrt{(-25)}$=(-3)×(-5) | D. | $\sqrt{1{3}^{2}-1{2}^{2}}$=$\sqrt{(13+12)(13-12)}$=$\sqrt{25}$=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,A(-2,3),B(-3,1),C(-1,2).
如图,△ABC中,A(-2,3),B(-3,1),C(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A市 | B市 | C市 | |
| D市 | 200元/台 | 300元/台 | 400元/台 |
| E市 | 800元/台 | 700元/台 | 500元/台 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
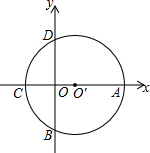 如图,在平面直角坐标系中,⊙Oˊ与两坐标轴分别交于A、B、C、D四点,已知A(6,0),C(-2,0).则点B的坐标为(0,-2$\sqrt{3}$).
如图,在平面直角坐标系中,⊙Oˊ与两坐标轴分别交于A、B、C、D四点,已知A(6,0),C(-2,0).则点B的坐标为(0,-2$\sqrt{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com