
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-4)^{2}}$=2 | B. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | C. | ($\sqrt{2}$)2=4 | D. | $\sqrt{6}$÷$\sqrt{2}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):| 运动员 环数 次数 | 1 | 2 | 3 | 4 | 5 |
| 甲 | 10 | 8 | 9 | 10 | 8 |
| 乙 | 10 | 9 | 9 | a | b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
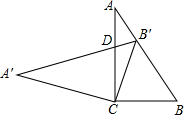 在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=0.35.
在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=0.35.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
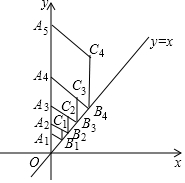 如图,在平面直角坐标系中,点A1的坐标为(0,1),过点A1作直线y=x的垂线,垂足为点B1,以A1B1为边作菱形A1B2C2A3,使得点A2落在y轴上,延长A2C1交直线于点B2,再以A2B2为边作菱形A2B2C2A3,使得点A3落在y轴上…按此作法继续作菱形,则点A2017的坐标是[0,(1+$\frac{\sqrt{2}}{2}$)2016].
如图,在平面直角坐标系中,点A1的坐标为(0,1),过点A1作直线y=x的垂线,垂足为点B1,以A1B1为边作菱形A1B2C2A3,使得点A2落在y轴上,延长A2C1交直线于点B2,再以A2B2为边作菱形A2B2C2A3,使得点A3落在y轴上…按此作法继续作菱形,则点A2017的坐标是[0,(1+$\frac{\sqrt{2}}{2}$)2016].查看答案和解析>>
科目:初中数学 来源: 题型:填空题
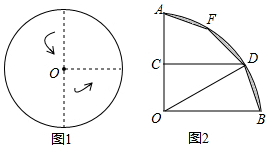 如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.
如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
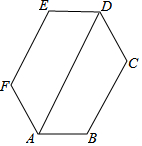 如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com