
甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
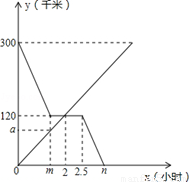
(1)a=90,m=1.5,n=3.5。
(2)y与x的关系式为
(3)乙车行驶了1小时或3小时
【解析】
试题分析:(1)∵甲车途径C地时休息一小时,∴2.5﹣m=1。∴m=1.5。
∵乙车的速度为: ,即
,即 ,解得a=90。
,解得a=90。
甲车的速度为: ,解得n=3.5。
,解得n=3.5。
∴a=90,m=1.5,n=3.5。
(2)分休息前,休息时,休息后三个阶段,利用待定系数法求一次函数解析式解答。
(3)求出甲车的速度,然后分①相遇前两人的路程之和加上相距的120千米等于总路程列出方程求解即可;②相遇后,两人行驶的路程之和等于总路程加120千米,列出方程求解即可。
解:(1)a=90,m=1.5,n=3.5。
(2)设甲车的y与x的函数关系式为y=kx+b(k≠0),
①休息前,0≤x<1.5,函数图象经过点(0,300)和(1.5,120),
∴ ,解得
,解得 。
。
∴y=﹣120x+300,
②休息时,1.5≤x<2.5,y=120。
③休息后,2.5≤x≤3.5,函数图象经过(2.5,120)和(3.5,0),
所以, ,解得
,解得 。
。
∴y=﹣120x+420。
综上所述,y与x的关系式为 。
。
(3)设两车相距120千米时,乙车行驶了x小时,甲车的速度为:(300﹣120)÷1.5=120千米/时。
①若相遇前,则120x+60x=300﹣120,解得x=1。
②若相遇后,则120(x﹣1)+60x=300+120,解得x=3。
∴两车相距120千米时,乙车行驶了1小时或3小时。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| A、4倍 | B、3倍 | C、2倍 | D、1.5倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:
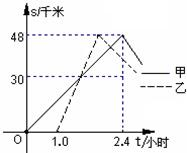 以30千米/小时的速度返回.请根据图象中的数据回答:
以30千米/小时的速度返回.请根据图象中的数据回答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com