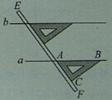
如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是：
A．同位角相等，两直线平行
B．内错角相等，两直线平行
C．两直线平行，同位角相等
D两直线平行，内错角相等．
 |
科目：初中数学 来源： 题型：
如果一个多
面体的一个面是多边形，其余各面是有一个公共顶点的三角形，那么这个多面体叫做棱锥。如图是一个四棱柱和一个六棱锥，它们各有12条棱，下列棱柱中和九棱锥的棱数相等的是
A. 五棱柱 B. 六棱柱 C. 七棱柱 D. 八棱柱
查看答案和解析>>
科目：初中数学 来源： 题型：
类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形” ．
（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，
∠B=80°．求∠C，∠D的度数．
（2）在探究“等对角四边形”性质时：
①小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．请你证明此结论；
②由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等” ．你认为她的猜想正确吗？若正确，请证明；若不正确，请举出反例．
(3)已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4．
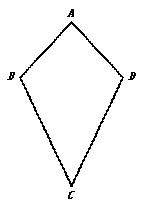求对角线AC的长．
| |||
| |||
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在矩形ABCD中，AD=8，E是边AB上一点，且AE=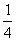
AB，⊙O经过点E，与边CD所在直线相切于点G（∠GEB为锐角），与边AB所在直线相较于另一点F，且EG：E
F=
。当边AD或BC所在的直线与⊙O相切时，AB的长是 
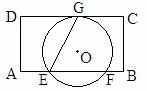
查看答案和解析>>
科目：初中数学 来源： 题型：
勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感。他惊喜地发现：当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明。下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：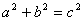
。
证明：连结DB，过点D作BC边上的高DF，
则DF=EC=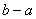
，
∵ 
，
又∵
，
∴ 
，
∴
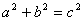
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°。
求证：。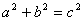
证明：连结
∵ 
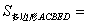
又∵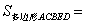 
∴
∴ 。
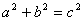查看答案和解析>>
科目：初中数学 来源： 题型：
有19位同学参加歌咏比赛，成绩互不相同，前10名的同学进入决赛.某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学成绩的
A．平均数 B．中位数 
C．众数 D．方差
查看答案和解析>>
科目：初中数学 来源： 题型：
，四边形ABCD是矩形，把矩形沿AC折叠，点B落在点E处，AE与DC的交点为O, 连接DE．
（1）求证：∆ADE≌∆CED; 
（2）求证： DE∥AC．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
如图，平行于BC的直线DE把△ABC分成的两部分面积相等.则
=___________.
，结果是（ ）．
（B）
（C）
（D）