
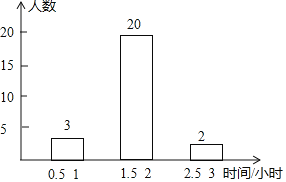
【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,学校随机抽查了部分学生在这次活动中做家务的时间,并绘制了如下的频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
等级 | 做家务时间(小时) | 频数 | 百分比 |
A | 0.5≤x<1 | 3 | 6% |
B | 1<x<1.5 | a | 30% |
C | 1.5≤x<2 | 20 | 40% |
D | 2≤x<2.5 | b | m |
E | 2.5≤x<3 | 2 | 4% |
(1)这次活动中抽查的学生有______人,表中a=______,b=______,m=______,并补全频数分布直方图;
(2)若该校七年级有700名学生,请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人?
【答案】(1)50,15,10,20%;(2)大约有490人
【解析】
(1)根据第一组的频数是3,百分比是6%,求得数据总数,再用数据总数乘以第二百分比率可得a的值,再用总人数-各个组人数可得b,根据百分率之和为1,求出m即可;
(2)利用总数700乘以做家务时间不足2小时而又不低于1小时的所占的百分比即可.
(1)总人数=3÷6%=50(人),a=50×30%=15,b=50-3-15-20-2=10,m=1-6%-30%-40%-4%=20%.
故答案为:50,15,10,20%;
(2)700×70%=490(人),
∴该校七年级有700名学生,请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有490人


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P的坐标为(m,n),则向量![]() 可以用点P的坐标表示为
可以用点P的坐标表示为![]() =(m,n);已知
=(m,n);已知![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),若x1x2+y1y2=0,则
=(x2,y2),若x1x2+y1y2=0,则![]() 与
与![]() 互相垂直.
互相垂直.
下面四组向量:①![]() =(3,﹣9),
=(3,﹣9),![]() =(1,﹣
=(1,﹣![]() );
);
②![]() =(2,π0),
=(2,π0),![]() =(2﹣1,﹣1);
=(2﹣1,﹣1);
③![]() =(cos30°,tan45°),
=(cos30°,tan45°),![]() =(sin30°,tan45°);
=(sin30°,tan45°);
④![]() =(
=(![]() +2,
+2,![]() ),
),![]() =(
=(![]() ﹣2,
﹣2,![]() ).
).
其中互相垂直的组有( )
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知:如图1,等边△A1A2A3内接于⊙O,点P是![]() 上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:
上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:![]() 是定值.
是定值.
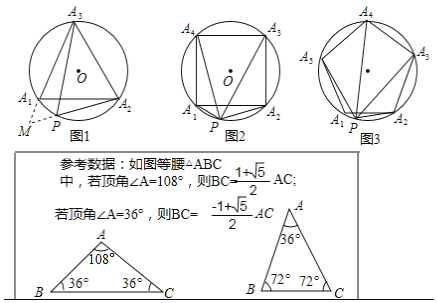
(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1,∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M

∴PA3=MA2=PA2+PM=PA2+PA1.
∴![]() ,是定值.
,是定值.
(2)延伸:如图2,把(1)中条件“等边△A1A2A3”改为“正方形A1A2A3A4”,其余条件不变,请问:![]() 还是定值吗?为什么?
还是定值吗?为什么?
(3)拓展:如图3,把(1)中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”,其余条件不变,则![]() = (只写出结果).
= (只写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
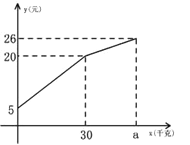
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
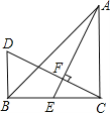
【题目】如图,△ABC中,∠ACB=90°,AC=BC,E是BC边上的一点,连接AE,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:△ACE≌△CBD;
(2)若BE=3![]() ,AB=6
,AB=6![]() ,求点E到AB的距离.
,求点E到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在五边形 ABCDE中,AB=AC=AD=AE,且AB//ED,∠EAB=120°,则∠DCB的度数是( )

A. 120°B. 130°C. 140°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理![]() 、
、![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元;
型净水器的进价各是多少元;
(2)槐荫公司计划购进![]() 、
、![]() 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时![]() 型净水器每台售价2500元,
型净水器每台售价2500元,![]() 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售![]() 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献![]() 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的AC的长;
,请直接写出所有满足条件的AC的长;
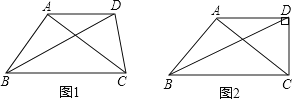
![]() 如图1,在四边形ABCD中,
如图1,在四边形ABCD中,![]() ,对角线BD平分
,对角线BD平分![]() ,
,![]() 求证:
求证:![]() 是比例三角形.
是比例三角形.
![]() 如图2,在
如图2,在![]() 的条件下,当
的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com