

分析 (1)根据题意可以求得∠B的度数,∠DFC的度数,从而可以求得∠AME的度数;
(2)根据题意可以分两种情况,一种是DM与线段AB相交,一种是DF与AB的延长线相交,分别针对两种情况再讨论,画出相应的图形,求出相应的t的值;
(3)根据题意可以分两种情况,一种是DM与线段AB相交,一种是DF与AB的延长线相交,然后根据题意可以分别求出两种情况下S与t的函数关系式.
解答 解:(1)在Rt△ABC中,tan∠B=$\frac{AC}{BC}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠B=30°,
在Rt△DEF中,∠D=30°,
∴∠DFC=60°,
∴∠FMB=∠DFC-∠B=30°,
∴∠AMF=180°-∠FMB=150°;
(2)∵BC=6,点P为线段BC的中点,
∴BP=3,
(ⅰ)若点M在线段AB上,
①当PB=PM时,PB=PM=3,
∵DE=3$\sqrt{3}$,∠D=30°,
∴EF=DE•tan30°=3,
∴此时t=0;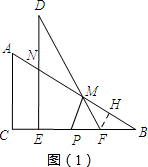
②如右图(1)所示
当BP=BM时,BP=BM=3,
∵∠B=30°,∠DFE=60°,
∴∠FMB=30°,
∴△BMF为等腰三角形.
过点F作FH⊥MB于H,则BH=$\frac{1}{2}$BM=$\frac{3}{2}$,
在Rt△BHF中,∠B=30°,
∴BF=$\sqrt{3}$,
∴t=3-$\sqrt{3}$;
③如右图(2)所示,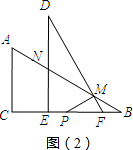
当MP=MB时,∠MPB=∠B=30
∵∠MFP=60°,
∴PM⊥MF,∠BMF=30°
∴FB=FM,
设FB=x,则FM=x,PF=2x.
∴3x=3,x=1
∴t=2;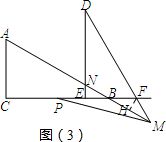
(ⅱ)若点M在射线AB上,
如右图(3)所示,
∵∠PBM=150°
∴当△PBM为等腰三角形时,有BP=BM=3
∵△BFM为等腰三角形,
∴过点F作FH⊥BM于H,则BH=$\frac{1}{2}$BM=$\frac{3}{2}$,
在Rt△BHF中,∠FBH=30°
∴BF=$\sqrt{3}$,
∴t=3+$\sqrt{3}$,
综上所述,t的值为0,3-$\sqrt{3}$,2,3+$\sqrt{3}$.
(3)当0<t≤3时,BE=6-t,NE=$\frac{\sqrt{3}}{3}$(6-t),
∴${S}_{△BEN}=\frac{1}{2}•(6-t)•\frac{\sqrt{3}}{3}(6-t)$=$\frac{\sqrt{3}}{6}(6-t)^{2}$,
过点F作FH⊥MB于H,如右图(1)所示,
∵FB=3-t
∴HF=$\frac{1}{2}$(3-t),HB=$\frac{\sqrt{3}}{2}$(3-t),MB=$\sqrt{3}$(3-t),
∴${S}_{△BMF}=\frac{1}{2}•\sqrt{3}(3-t)•\frac{1}{2}(3-t)$=$\frac{\sqrt{3}}{4}(3-t)^{2}$,
∴S=S△BEN-S△BMF=$\frac{\sqrt{3}}{6}(6-t)^{2}-\frac{\sqrt{3}}{4}(3-t)^{2}$=$-\frac{\sqrt{3}}{12}{t}^{2}-\frac{\sqrt{3}}{2}t+\frac{15\sqrt{3}}{4}$,
当3<t≤6时,BE=6-t,NE=$\frac{\sqrt{3}}{3}$(6-t),如右图(4)所示,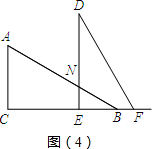
∴S=${S}_{△BEN}=\frac{1}{2}×(6-t)×\frac{\sqrt{3}}{3}(6-t)$=$\frac{\sqrt{3}}{6}{t}^{2}-2\sqrt{3}t+6\sqrt{3}$,
由上可得,当0<t≤3时,S=$-\frac{\sqrt{3}}{12}{t}^{2}-\frac{\sqrt{3}}{2}t+\frac{15\sqrt{3}}{4}$,
当3<t≤6时,S=$\frac{\sqrt{3}}{6}{t}^{2}-2\sqrt{3}t+6\sqrt{3}$,
即S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{12}{t}^{2}-\frac{\sqrt{3}}{2}t+\frac{15\sqrt{3}}{4}}&{0<t≤3}\\{\frac{\sqrt{3}}{6}{t}^{2}-2\sqrt{3}t+6\sqrt{3}}&{3<t≤6}\end{array}\right.$.
点评 本题考查三角形综合题,解题的关键是明确题意,画出相应的图形,找出所求问题需要的条件,利用数形结合的思想、特殊角的三角函数值、分类讨论的数学思想解答本题.


科目:初中数学 来源:2016-2017学年四川省成都市金堂县八年级上学期期末考试数学试卷就(解析版) 题型:解答题
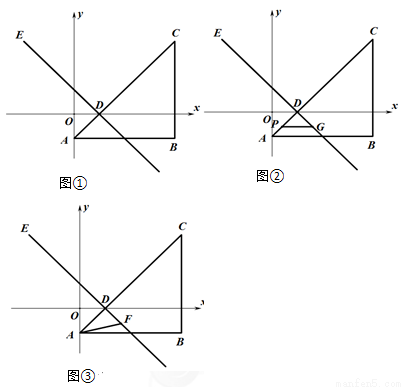
如图①,等腰直角三角形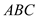 的顶点
的顶点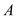 的坐标为
的坐标为 ,
,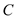 的坐标为
的坐标为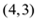 ,直角顶点
,直角顶点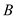 在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.
在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.
(1)直接写出点B、D、E的坐标并求出直线DE的解析式.
(2)如图②,点P以每秒1个单位的速度沿线段AC从点A运动到点C的过程中,过点P作与x轴平行的直线PG,交直线DE于点G,求与△DPG的面积S与运动时间t的函数关系式,并求出自变量t的取值范围.
(3)如图③,设点F为直线DE上的点,连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FE以每秒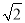 个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.
个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省成都市金堂县八年级上学期期末考试数学试卷就(解析版) 题型:填空题
已知:m、n为两个连续的整数,且m<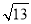 <n,则mn的平方根 =__.
<n,则mn的平方根 =__.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
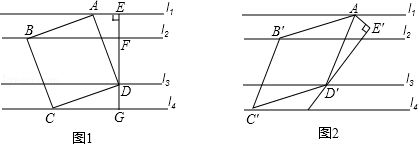
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
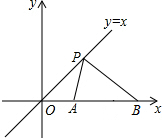 在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(6,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{10}$.
在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(6,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com